公司新闻

卷积：从推理引擎优化和硬件优化角度理解

网上许多卷积的学习资料大多比较零散，本文结合网络上搜集的一些资料，从推理引擎优化和硬件优化角度去了解和总结深度学习中卷积的各个方面的优化手段。阅读本文需要算法基础知识，计算机体系结构和推理引擎的基础知识即可。文章中有什么不正确地方，希望大家及时支持，大家共同进步。

从数字信号处理引出卷积

在数字信号处理中，当一个系统是线性时不变系统时，引出了卷积；

给的输入增大，输出也线性增大，这叫线性。t时刻的输入比t+1时刻的输入先得到结果，这叫时不变。

卷积是线性和时不变性的一个直接结果。卷积的公式为：

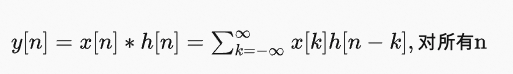
即如果已知所有的x[n]和h[n]就可由卷积公式求出输出序列y[n]，入下图可以形象看出卷积计算的整个过程。

卷积的重要的物理意义是：一个函数（如：单位响应）在另一个函数（如：输入信号）上的加权叠加。

深度学习中的卷积

CNN中的基础卷积操作，是由一组具有固定窗口大小且带可学习参数(learnable paramerters)的卷积核所组成，可用于提取特征。如下图所示，卷积的过程是通过滑动窗口从上到下，从左到右对输入特征图进行遍历，每次遍历的结果为相应位置元素的加权求和。

从算法角度来讲，卷积是参数共享的、平移等变的。
从计算角度来讲，卷积操作是卷积核矩阵与被选中特征矩阵区域的元素*乘累加*操作。

从神经网络前向推理看看卷积(Kernels)操作

输入tensor(N*Ci*H*W) -> CONV(Co*Ci*Kw*Kh) -> 输出tensor N*Co*H*W
这里假设是输入输出featuremap 大小不变的卷积运算。

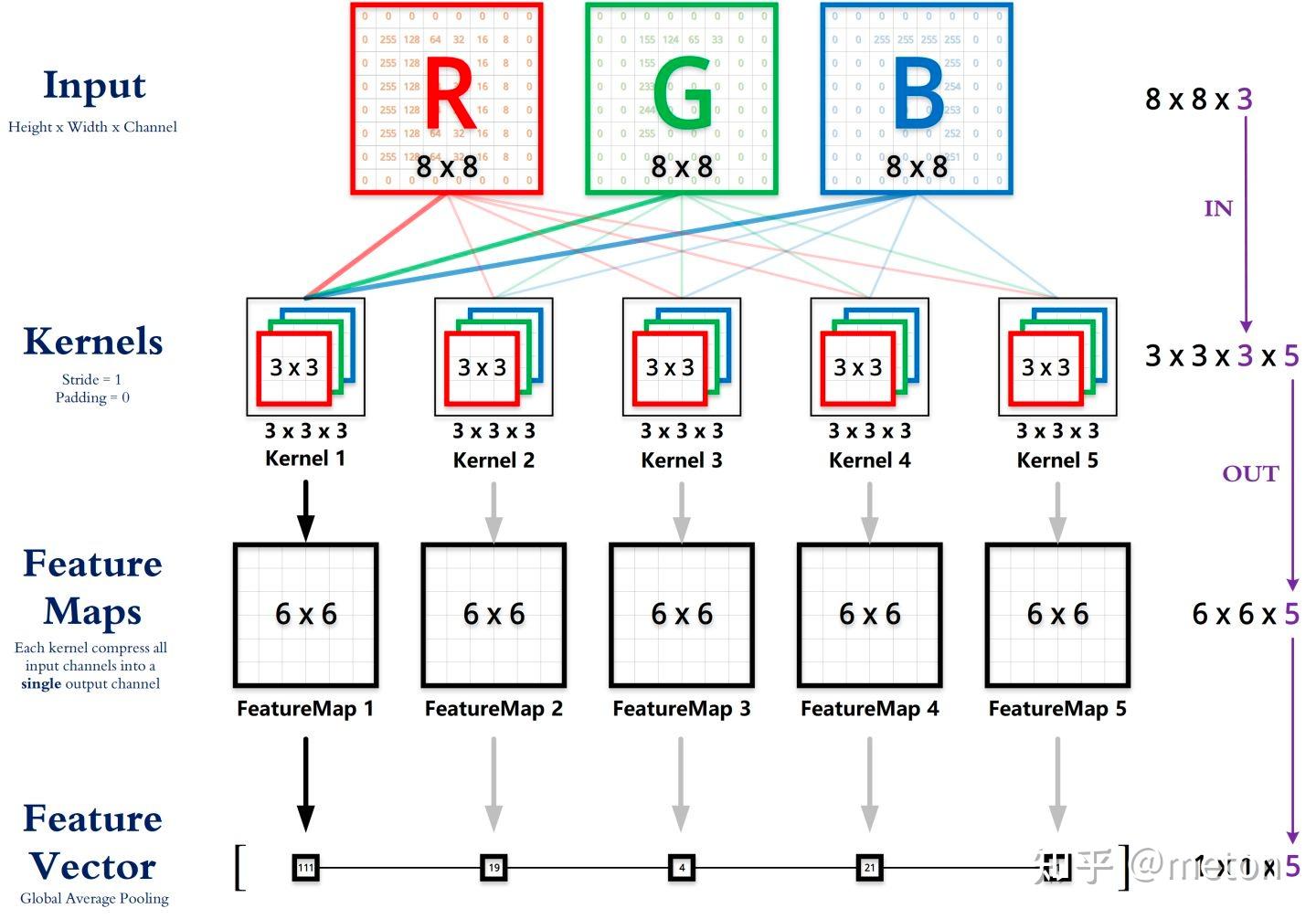
在大卷积核前应用1X1卷积，可以灵活地缩减feature map通道数（同时1X1卷积也是一种融合通道信息的方式），最终达到减少参数量和乘法操作次数的效果。

group convolution，将feature map的通道进行分组，每个filter对各个分组进行操作即可，像上图这样分成两组，每个filter的参数减少为传统方式的二分之一（乘法操作也减少）。该种卷积应用于ShuffleNet。

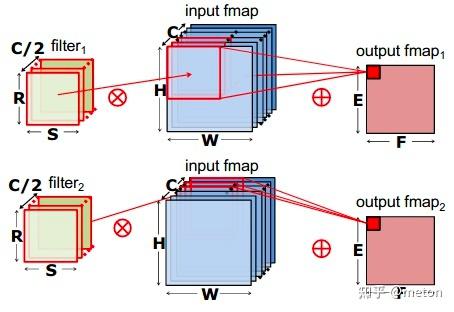
depthwise convolution，是组卷积的极端情况，每一个组只有一个通道，这样filters参数量进一步下降。

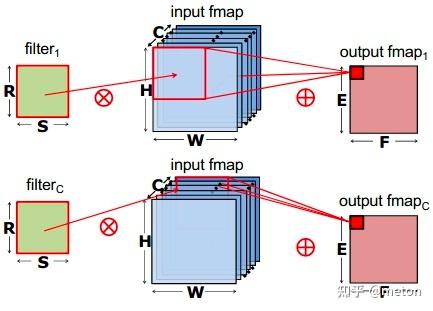
将原本卷积操作分解成两步，先进行 depthwise convolution，之后得到的多个通道的feature map再用一个1X1卷积进行通道信息融合，拆解成这样两步，卷积参数也减少了。对比如下：

普通卷积

输入tensor(N*Ci*H*W) -> CONV(Co*Ci*Kw*Kh) -> 输出tensor N*Co*H*W

深度卷积+1x1卷积

输入tensor(N*Ci*H*W) -> DWCONV(Ci*1*Kw*Kh)->中间tensor N*Ci*H*W ->PWCONV(Co*Ci*1*1)->输出tensor N*Co*H*W

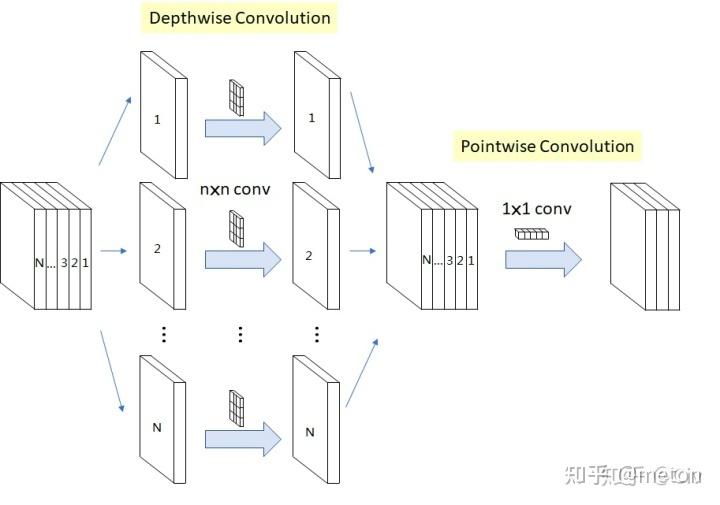
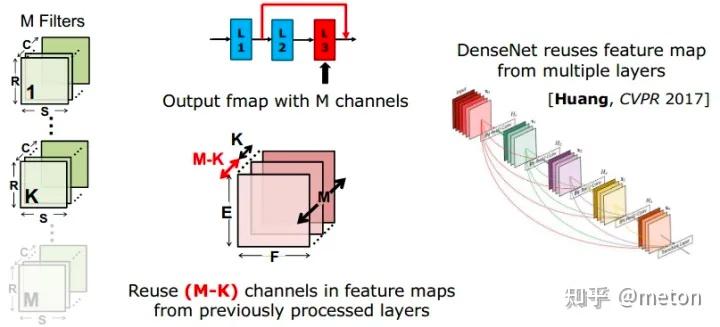
也就是减少Co*Ci*Kw*Kh 中的Co，直接减少的filter数目虽然可以减少参数，但是导致每层产生的feature map数目减少，网络的表达能力也会下降不少。一个方法是像DenseNet那样，一方面减少每层filter数目，同时在每层输入前充分重用之前每一层输出的feature map。

在不增加参数情况下增加感受野

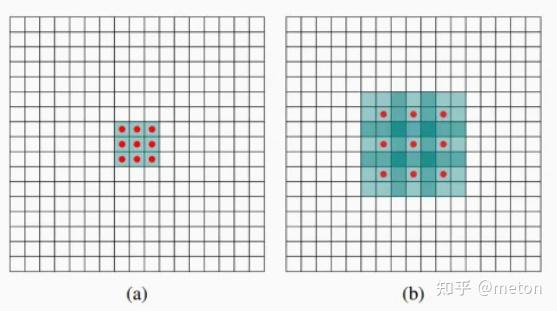
(a) 图对应3x3的1-dilated conv，和普通的卷积操作一样。

(b) 图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，也就是对于一个7x7的图像patch，只有9个红色的点和3x3的kernel发生卷积操作，其余的点略过。也可以等效理解为kernel的size为7x7，但是只有图中的9个点的权重不为0，其余都为0。可以看到虽然kernel size只有3x3，但是这个卷积的感受野已经增大到了7x7。

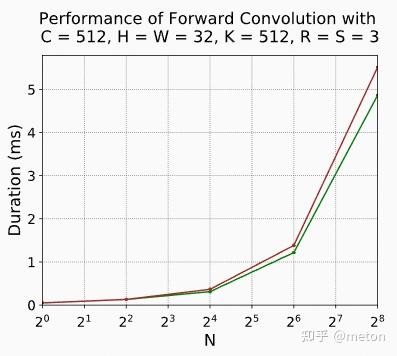
膨胀卷积在计算时候并没有增加计算量，因此下图的普通卷积核绿色以及膨胀卷积（红色）没有展现出明显的速度差距。（实验数据来自NV平台的卷积测试(https://docs.nvidia.com/deeplearning/performance/dl-performance-convolutional/index.html#tensor-layout)）

其核心思想是通过将原始卷积分解，该算法将三个分别具有正方形，水平和垂直核的卷积分支的输出求和。从而在保持精度相当的情况下降低参数量和计算量，形式上利用到前面提到的空间可分离卷积。推理引擎不常见这类卷积，不赘述。

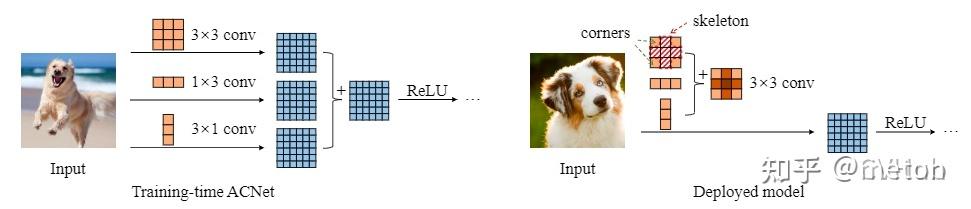
对于性能优化工程是来讲，卷积运算本质是tensor运算，因此从推理优化角度来看，卷积分类可以从卷积tensor本身的输入输出特点来分类。

下图展示了典型的Resnet50模型的卷积参数变化情况，其中包含了大图少通道和小图多通道两种类型。特征图的三个尺寸“长x宽x通道”标注于特征图的上方，如224x224x3、56x56x64等。卷积核尺寸“长x宽”标注于卷积核的下方，如7x7、1x1等。

大图少通道类型：这种类型的卷积一般存在于神经网络的开始阶段，它的特点是特征图的长和宽较大（即大图），比如224，但是通道数目比较小（即多通道），比如3。这种卷积类型属于访存密集型运算，一般对于针对计算密集设计的硬件(如TensorCore)，这种类型得不到充分的发挥。一般网络推理的内存峰值发生可能发生在这个地方。
小图多通道类型：这种类型的卷积存在于神经网络的中间和末尾阶段，它的特点是特征图的长和宽较小（即小图），比如56/28/14等，但是通道数目比较大（即多通道），比如64/128/256等。这种卷积类型也属于访存密集型计算，由于特征图的长和宽较小，无法充分利用GPU的并行计算资源。可以从挖掘reduce维度（K维度）的并行性来充分利用GPU的硬件资源。
多图多通道类型: 这种类型的卷积是小图多通道类型的多batch情况。当batch增多时并行性也得到增加。这种卷积类型属于计算密集型运算，比较适合发挥Tensor Core的计算能力。

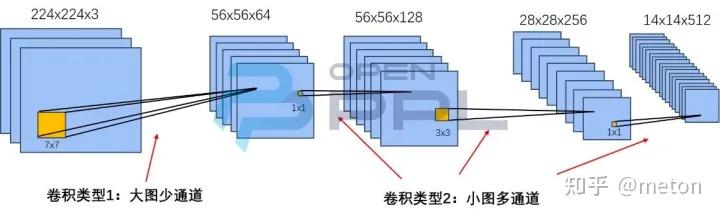
根据要处理的tensor本身的类别不同(分辨率、通道数、卷积核kernel大小等)，推理引擎往往会精细地选择不同的卷积kernel实现，来取得比较优的效果。

在 CV 领域中，卷积计算是扩充像素的感受野的有效方法，模型大多数的计算量都是卷积操作贡献的。因此在 CV 模型的推理性能优化中，最重要的一项工作是对卷积的优化。各类推理引擎中，卷积优化的基本方法有：

直接卷积计算优化

该方法的计算过程为逐通道进行卷积滑窗计算并累加，该优化方法对卷积的参数敏感，为了达到最优的性能，会根据各个卷积参数分别进行 kernel 优化，通用性弱，但是在 Depthwise 的卷积中却是最高效的方法。

FFT 卷积计算优化

根据卷积的性质，利用傅立叶变换可以将卷积转换为频域上的乘法，在频域上的计算对应乘法，再使用傅立叶变换逆变换，就可以得到卷积对应的计算结果。该方法使用高性能的傅立叶变换算法，如 FFT，可以实现卷积计算的优化，算法性能完全取决于傅立叶变换的性能以及相应卷积参数。

Im2col+GEMM 卷积计算优化

由于卷积计算中有大量的乘加运算，和矩阵乘具有很多相似的特点，因此该方法使用 Im2col 的操作将卷积运算转化为矩阵运算，最后调用高性能的 Matmul 进行计算。该方法适应性强，支持各种卷积参数的优化，在通道数稍大的卷积中性能基本与 Matmul 持平，并且可以与其他优化方法形成互补。

Winograd 卷积计算优化

Winograd 方法是按照 Winograd 算法的原理将卷积运行进行转变，达到减少卷积运算中乘法的计算总量。其主要是通过将卷积中的乘法使用加法来替换，并把一部分替换出来的加法放到 weight 的提前处理中，从而达到加速卷积计算的目的。Winograd 算法的优化局限为在一些特定的常用卷积参数才支持。

Strassen 矩阵乘算法

Strassen 矩阵乘算法是一种快速矩阵乘法的算法，通过分治和递归的方式，将矩阵的乘法转化为子矩阵的运算。该算法的时间复杂度为 $O(n^{log_2 7})$，比传统的矩阵乘法 $O(n^3)$ 更加高效，适用于大规模的矩阵乘法计算。MNN目前有使用这种矩阵乘优化算法。

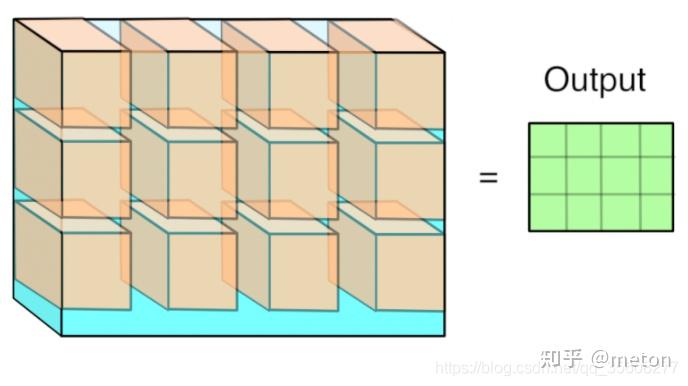
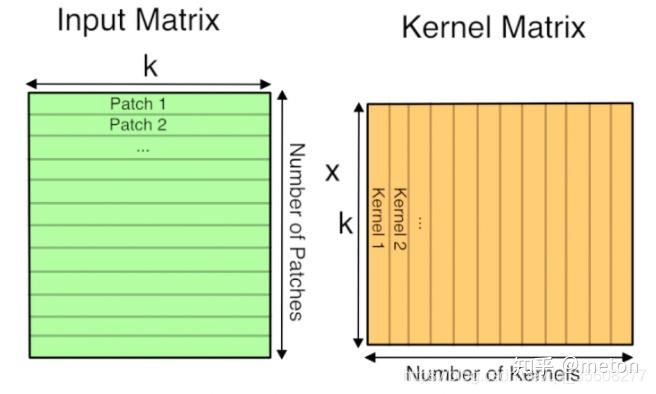
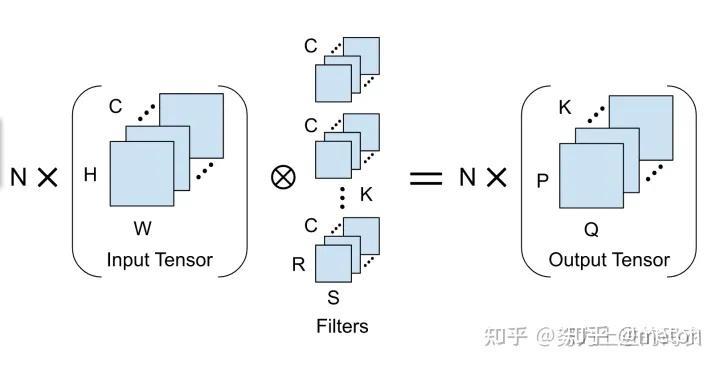
im2col 是计算机视觉领域中将图片的不同通道（channel）转换成矩阵的列（column）的计算过程。im2col可以将卷积操作转换为矩阵乘法GEMM运算，GEMM加速已经是一个成熟领域，将卷积运算等效成GEMM计算，就可以白嫖矩阵优化领域许多成熟的Kernel实现，比如NV的cuDNN, matlab软件中的矩阵运算toolkit, 比较早是Caffe框架中引入im2col方法，后被许多框架实现借鉴。
具体来说，im2col将输入图像的每一个局部窗口（即卷积核大小的滑动窗口）转换为一个行向量，并将所有这样的列向量拼成一个矩阵。在矩阵乘法运算中，卷积核也被转换为一个行向量，并与输入矩阵相乘，得到输出矩阵的每一个元素。这样，卷积操作就被转换为矩阵乘法运算。计算完毕后通过col2im 恢复出输出tensor。

多通道输入情况下的im2col示意图。

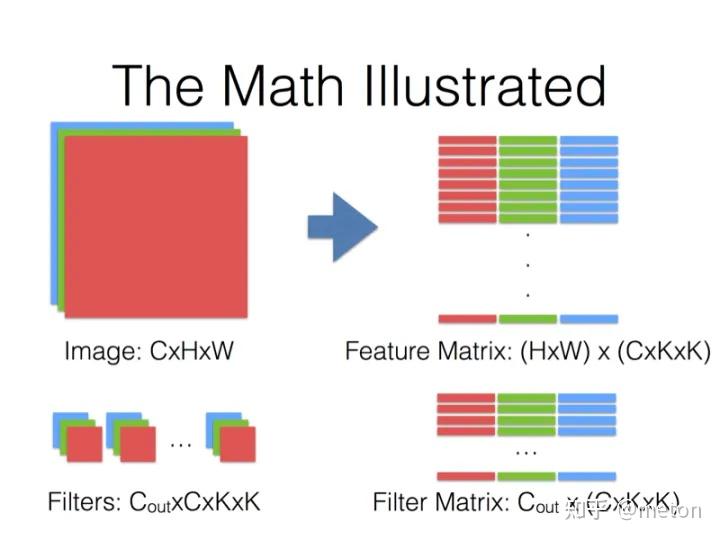
im2col 计算卷积使用 GEMM 的代价是额外的内存开销，输入会使用额外的 × 倍内存（空间换时间）。
需要注意的细节是：当卷积核尺寸是 1×1 时，由于不需要重排输入，GEMM 可以直接在原始输入上运行，并且不需要使用额外的内存。因此此时im2col转换减少额外数据冗余开销。

将卷积运算映射为矩阵运算。有两种映射方式，一种是显式矩阵乘卷积（explicit GEMM convolution），另一种是隐式矩阵乘卷积（implicit GEMM convolution）。二者的计算方式相同，区别在于是否需要额外的存储空间来放置临时数据。因此这只是工程实现上的一些差异。

显式矩阵乘是在临时空间内将卷积操作的特征图和卷积核转换为两个矩阵，即Im2Col操作。隐式矩阵乘通过索引计算省去了Im2Col操作，从而避免了开辟临时空间，这对于内存敏感的情况很有效。TensorRT和cutlass在Tensor Core计算单元上主要采用的是隐式矩阵乘算法。

以TensorRT中卷积运算为例，整个隐式矩阵乘卷积的算法流程如下图所示，其中，IH/IW/IC代表输入特征图的长，宽，通道，FH/FW代表卷积核的长和宽，OH/OW/OC代表输出特征图的长，宽，通道，Batch大小为N。X代表通道的数目，其含义可以参考TensorRT中提出的五维数据排布格式NCxHWX，将X个通道放在inner-most维度（X一般是mma指令k维度大小的倍数，如8/16/32/64等）。

GEMM在CPU端优化主要思想是：

1）利用数据分块以适配Cache的数据局部性来提高访存效率(数据重用 data reuse) 。

2）利用现有微架构能力(SIMD、多核、硬件流水线指令排布优化等)。

GEMM优化本质上优化循环体计算，下面从一个最Naive实现说起，逐步展示GEMM循环优化手段。

3层循环实现：

for (int m=0; m < M; m++){
  for (int n=0; n < N; n++){
    C[m][n]=0;
    for (int k=0; k < K; k++){
      C[m][n]+=A[m][k]* B[k][n];
    }
  }
}

在实际中，A，B，C矩阵往往非常巨大，直接使用最naive方式，会由于访存性能差以及计算操作多导致运行效率低。

要了解原因需要知道现有计算机微架构下，访存与计算的鸿沟，从这点再来理解为什么Naive实现访存性能差。

现代cpu架构中计算指令(ADD/MUL)和DRAM访存操作延时对比来看（相差多个数量级），上述第一点对于多层次存储架构的cpu来说，影响巨大。因此许多GEMM优化都在减少直接的DRAM访问下重要的功夫，那些写的难懂的数据重排代码都是为了提高访存效率。

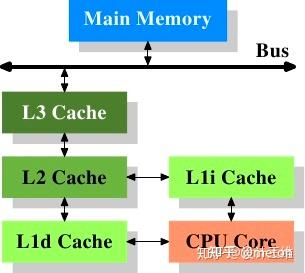
一个优化的思路就是在cpu寄存器和DRAM直接架设几个中间层，用于缓存中间数据，这些中间层的访问速度要很快，比DRAM要快。这就是现代处理器架构中的Cache的设计思路。

Cache基础概述

cache参与构成现代处理器的多层次存储结构（参考下图，CPU寄存器--L1 cache--L2--L3--主存--磁盘等大容量存储器），是除寄存器外最靠近CPU核的存储单元，通常由SRAM组成。
L1 cache离CPU核最近，存储信息的读取速度接近CPU核的工作速度，容量较小，一般分成I-cache和D-cache两块，分别存储指令和数据；L2 cache比L1更远，速度慢一些，但是容量更大，不分I-cache和D-cache；L3更慢、更大，现在流行多核处理器，L3一般由多个处理器核共享，而L1、L2是单核私有的。
cache容量较小，所以数据需要按照一定的规则从主存映射到cache。一般把主存和cache分割成一定大小的块，这个块在主存中称为data block，在cache中称为cache line。举个例子，块大小为1024个字节，那么data block和cache line都是1024个字节。当把主存和cache分割好之后，我们就可以把data block放到cache line中，而这个“放”的规则一般有三种，分别是“直接映射”、“组相联”和“全相联”。
Cache Line可以理解为CPU Cache中的最小缓存单位。其大小是以突发读发写周期的大小为基础的。目前主流的CPU Cache的Cache Line大小都是64字节（一个浮点数4字节，可以存放 64/4=16个浮点数）。CPU不是按字节访问内存，而是以64字节为单位的块(chunk)拿取，称为一个cache line。当你读一个特定地址的内存时，整个Cache Line大小的内存将从主存换入缓存，并且这是cpu访问同一个Cache Line内的其它值开销是很小的。

循环优化的核心在于：

1.提高数据重用(data reuse)。重用的数据可以维持在Cache中，cpu可以更加快速取到，而不用去取。

2.减少Cache miss，提高访存效率。

数据重用是什么？

关于卷积中的数据重用，用下面的图来解释:

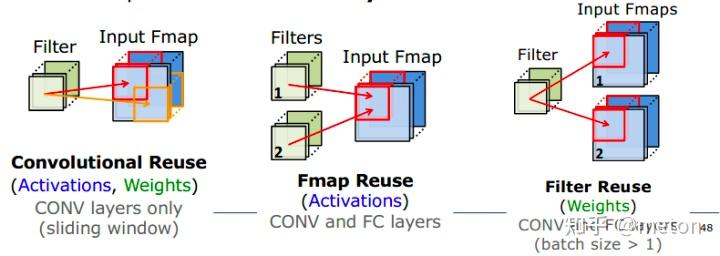
卷积神经网络三个角度复用，一是复用权重；二是复用激活（也就是feature map）；三是复用两者。不同的复用策略，可以引申出不同设计架构和取数策略。

常见循环优化

循环展开：将循环体中的多个迭代合并成一个，减少迭代次数，提高代码执行效率。
循环合并：将多个循环合并成一个循环，避免循环嵌套，提高代码执行效率。
利用循环不变量：在循环中找出不会变化的变量，减少不必要的计算，提高执行效率。
数据重用：将循环中的计算结果保存下来，避免重复计算，提高执行效率。
并行化：将循环中的迭代分成多个部分，分别在多个处理器上并行执行，提高代码执行效率。
数据预取：预先将循环中需要的数据加载到高速缓存中，减少内存访问时间，提高执行效率。
消除死循环：避免死循环的发生，提高代码的可靠性和执行效率。
消除循环中的函数调用：避免在循环中调用函数，减少函数调用的开销，提高执行效率。
利用矢量化指令：使用矢量化指令对数据进行处理，减少循环次数，提高执行效率。
循环展开加矢量化：将循环展开和矢量化结合起来，进一步提高执行效率。

各类推理引擎中的CPU卷积优化实现，最终都落到优化循环中，而多么复杂的循环优化，都基本离不开以上几种思想。

关于循环优化衍生出两大优化的派系：

手写Kernel派: 对于不同输入规模，不同参数设计不同的Kernel代码，实际中根据经验去调用不同的Kernel，以cuDNN为代表。
Kernel生成派：利用for循环代码模板，在硬件上进行参数搜索得到适合的Kernel参数，生成Kernel代码，以TVM为代表。

相比于直接的naive实现，常见的优化是分tile计算

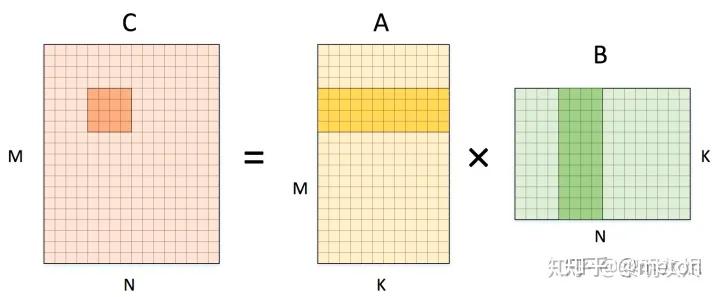
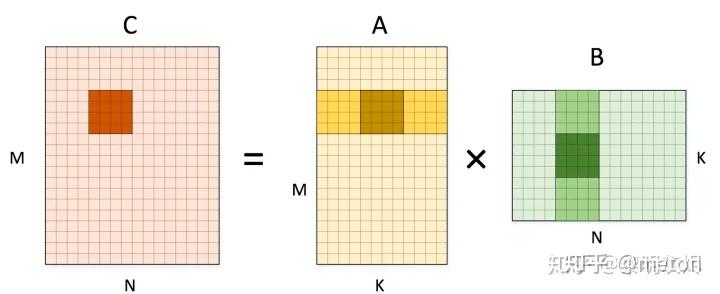
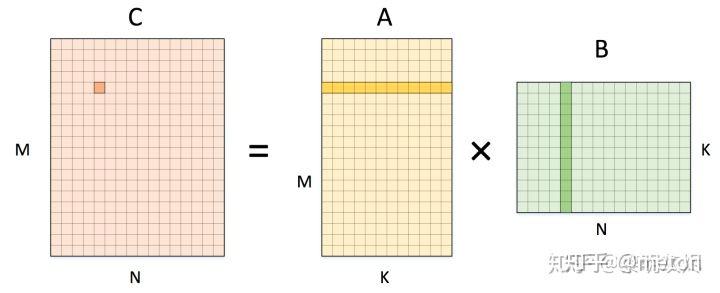
对于输出矩阵C，分块的思想是每次计算得到C的一小块结果(4x4小块)，这个4x4小块是由右边A和B中的浅阴影小区域分别进行矩阵运行得到的，而这两个小矩阵区域又可以拆分成多个4x4块进行矩阵(最深阴影小块)进行小矩阵运行并叠加而成。类似分块的套娃运算，此时来看，A和B的深色小块是可以装入Cache进行数据复用的，减少了向DRAM直接取数的大开销。

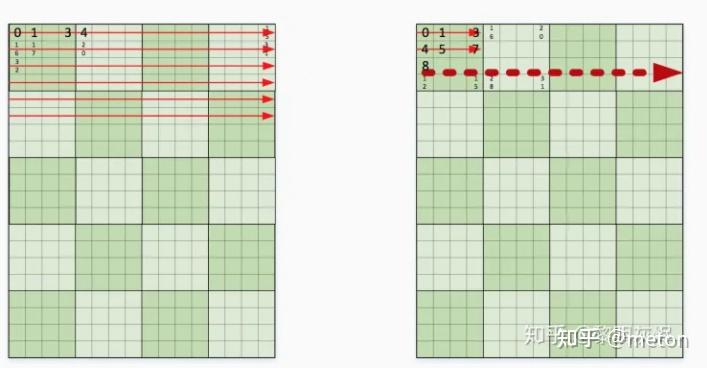
图中两者都是行优先的内存排列，区别在于左侧小方块内部是不连续的，右侧小方块内部是连续的。图中用几个数字标记了各个元素在整个内存中的编号。

想象一下在这两者不同内存组织方式的输入输出中访存，每次向量化内存加载仍是 4 个元素。对于一个局部计算使用到的小方块，左侧四次访存的内存都是不连续的，而右侧则是连续的。当数据规模稍大（一般情况肯定足够大了），左侧的连续四次向量化内存加载都会发生高速缓存缺失（cache miss），而右侧只会有一次缺失。

在常规的数据规模中，由于左侧会发生太多的高速缓存缺失，又由于矩阵乘这样的计算对数据的访问具有很高的重复性，将它重排成右侧的内存布局减少高速缓存缺失，可显著地改进性能。另一方面，矩阵乘中两个输入矩阵往往有一个是固定的参数，在多次计算中保持不变。那么可以在计算开始前将其组织成特定的形状，这种优化甚至可以将性能提高 2x。

在实际实现中，由于卷积核参数是事先知道的，因此可以在进行卷积计算前，对卷积参数矩阵进行数据重排，这个重排操作，只在离线进行一次，因此开销不大。

关于数据重排，多说一句

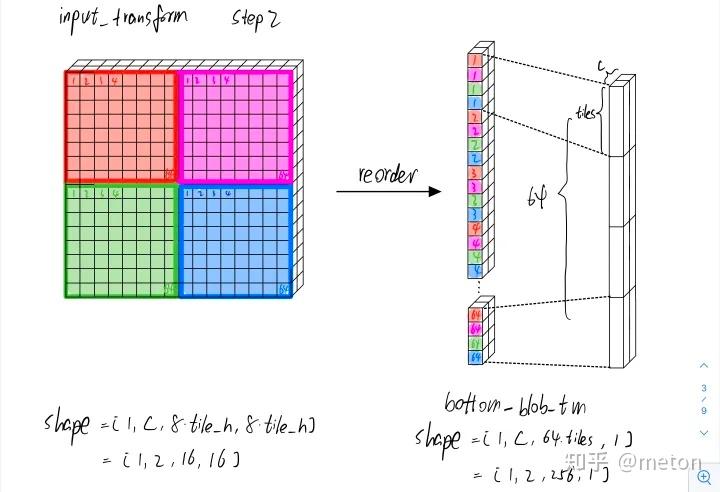
上面的图可能不太明显，我们以NCNN wingrad卷积中，构造input_transform矩阵时候进行的数据重排为例，来说明, 可以看到重排后，原先每一个tile相同位置的元素都汇集到一起，排布连续，那么后续计算如果每次都要处理四个tile的对应位置的元素，只需一次访存动作，四个元素就都在Cache line里面了。可以看到，数据重排的好处是增加了Cache取数的友好性。

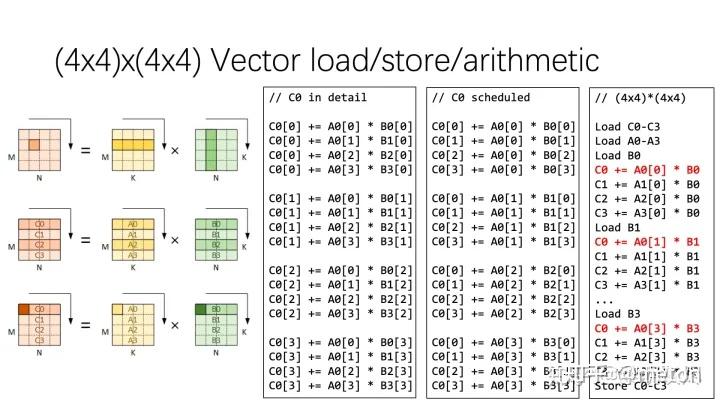
第一份代码实现 C0 in detail 是计算 C0 中四个输出元素的朴素方法的展开，连续四次计算得到一个 C0 元素的结果。

将计算过程稍作数据重排，即可得到 C0 scheduled 展示的计算，这里连续的四次计算分别处理了 C0 中四个元素的 1/4 结果。在连续的四次计算中，重排前只有对 A 的访存是连续的，重排后 A0和 B0的访存都是连续的。那么向量化这些访存和计算，即可得到第三列伪代码中红色 C0 部分。

而第三列是通过对 C1、C2、C3 进行类似的处理得到的。施行向量化操作后，原本需要 64 条计算指令的计算过程所需指令减少到 16 条，访存也有类似效果。而向量化对处理器资源的高效使用，又带来了进一步优化空间，例如可以一次计算 8×8 个局部输出。

cpu架构是支持向量操作，但是像cpu+gpu的模式，gpu本身支持tensor单元并行计算，因此单次可以并行的元素数目是要向量计算更多，因此对于大规模矩阵运行，tensor operations 是要比cpu的vector operations吞吐量更大的。

在深度学习中有两种内存排布方式，NCHW 和 NHWC。早期的caffe，tensorflow是以NHWC为主，因为他们开始主要支持的基于CPU的运算。后面的torch的内存模型以NCHW为主，因为在GPU上运算，NCHW更快。

NHWC，又称为“channel last”，在单线程下面比较适合CPU，排布方式为“RRRRRRGGGGGGBBBBBB”。在CPU的实现上，可以采用SSE或者AVX优化，pack 4或者8个字节进行运算。由于这种内存排布局部性更好，Cache Missing的情况更少。但是缺点也很明显，不利于做sum reduction。
NHWC，C在外层，内存排列方式为“RGBRGBRGB”。对于GPU而言，尤其是多线程下面做reduction是非常耗时的操作，NCHW其实更利于GPU做并行化计算，而且CUDA默认的内存模型就是NCHW。

由于NCHW，需要把所有通道的数据都读取到，才能运算，所以在计算时需要的存储更多。这个特性适合GPU运算，正好利用了GPU内存带宽较大并且并行性强的特点，其访存与计算的控制逻辑相对简单；

而NHWC，每读取三个像素，都能获得一个彩色像素的值，即可对该彩色像素进行计算，这更适合多核CPU运算，CPU的内存带宽相对较小，每个像素计算的时延较低。如果采用多线程编程实现，NCHW更容易进行代码实现，效率更高，而GPU正好是使用SIMT多线程架构。如果是纯单核做推断的话，采用NHWC更好。」

注意：NV GPGPU使用的SIMT架构，因此理论上更适合NCHW，但是现在的高性能NV计算卡往往带有专门的TensorCore硬件，这种相当于在原本GPU中嵌入了一个专门的矩阵运算单元，如果使用TensorCore来加速卷积运算的话，则其实NHWC更加友好，有官方实验数据为证，可见NCHW还是NHWC合适，其实是和硬件设计强相关。

对于CPU平台来说，不同的内存布局会影响计算运行时访问存储器和Cache的模式，特别是在运行矩阵乘时。本小节分析CPU平台中采用 Im2col 优化算法时计算性能性能和内存布局的关系。

首先考虑 NCHW 内存布局，将 NCHW 内存布局的卷积对应到矩阵乘=时，是卷积核（filter），是输入（input），各个矩阵的维度如图四所示。图中的 , , 用于标记矩阵乘，即

，同时标记出它们和卷积计算中各个维度的关系。

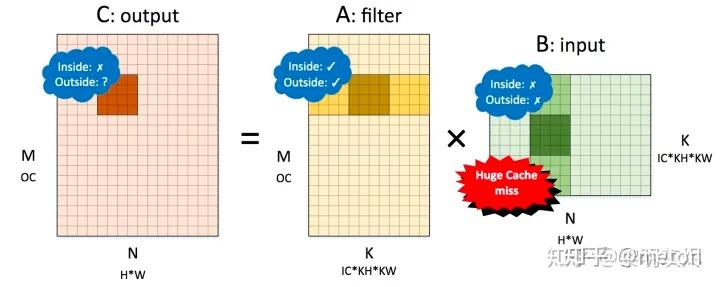
对该矩阵施行划分后，我们详细分析局部性的表现。其中 Inside 表示 4×4 小块矩阵乘内部的局部性，Outside 表示在削减(reduce)维度方向小块之间的局部性。

对卷积核A而言，如果没有进行数据重排布(前小节有讲)，其实小块内访存局部性较差，这和输出类似。当小块加载发生缓存缺失时，处理器会一次性加载一个缓存行（Cache line），这使得后续的若干个小块访存都能缓存命中（Cache hit），直到该缓存行全部命中后进入下一个缓存行的范围。因此小块外部局部性较好。但是事先对卷积参数进行patch数据重排，则reduce维度数据排布也是连续的，因此访存局部性也是好的。而且卷积参数是事先确定的，因此重排操作只需要做一次。
对输入而言，小块内访存局部性表现同样不好。然而不同于卷积核，小块中因缓存缺失加载到缓存中的缓存行数据只会被使用一次，因为这种内存布局中下一个小块的地址范围一般超出了一个缓存行。因此输入的几乎每次内存加载都会发生高速缓存缺失——Cache 没有起到加速的作用，每次访存都需要到内存取数据。

如果A和B矩阵角色互换呢？也就是说让A作为Input, B作为卷积核，情况分析如下：

对输入而言，小方块的内部局部性表现不是很好，因为几次向量加载都会发生缓存不命中；而外部局部性表现则较好，因为在reduce维度滑动使用的内存是连续的。这种表现和 NCHW 中卷积核的表现一样，整体来看都是对高速缓存比较友好的内存布局。
对卷积核而言，如果没有进行数据重排，则其实NHWC 的情况和 NCHW 中输入的情况类似，小块内和小块外的局部性都较差，因为都是列访问模式，访存局部性本身就差。但是由于卷积参数本身固定，因此可以离线对B矩阵进行数据重排，使得列访问的不连续通过重排变成连续，此时B矩阵小块内和小块reduce维度的访问都是访存友好的。

总结：

NHWC和NCHW哪个好并不能一概而论，要结合实际实现和硬件特点来讲。对于特定硬件，如果你的硬件访存是对NHWC友好，同时，卷积实现的数据计算过程和数据遍历过程是匹配NHWC的排布特点的(代码实际实现)，那么此时你的实现就会是最优的。
这里值得说明的是一般框架或引擎的运行都至少可分为两个阶段：准备阶段和运行阶段。一些模型的预处理工作可以放在准备阶段完成，例如重新排布卷积核的内存布局。

可以看到，NC4HW4的排列顺序是每4个channel顺序排列的，每4个channle作为一组，即C4，如果通道数量非4的整数呗，那就全补0。在每一组内，进行HWC来组织。类似图像中的RGBA方式。因此这一种可以看做是NCHW+NHWC的混合排布。NC4HWc4结构，在转换时候，最明显时候就是将每4个channel组合成一起，这也是最为便利并行以及对cache较为友好（在特定实现中）。

HWc4在进行naive卷积时候的计算过程：

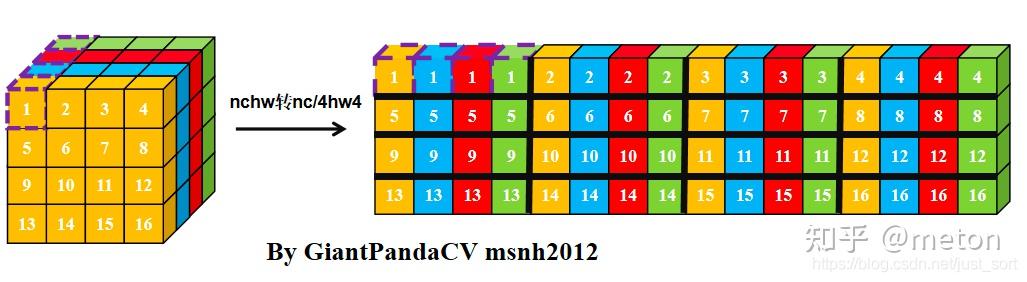
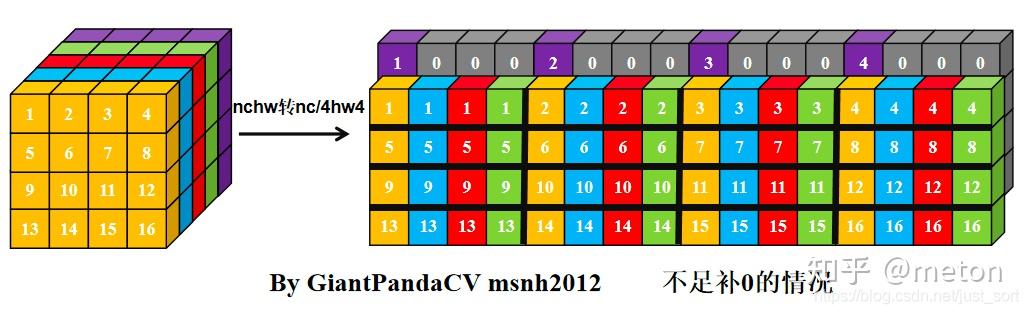
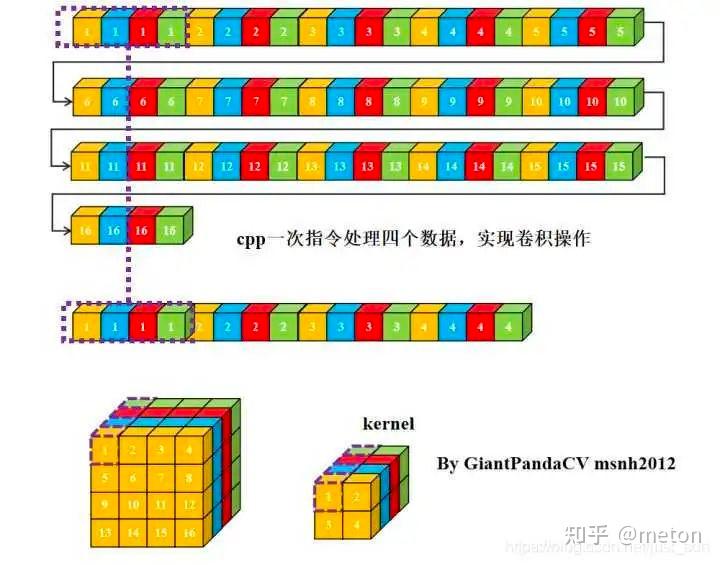
这里是按通道去做卷积操作，而由于通道元素本身在存储时候是连续的，因此使用HWc4去做最naive的卷积操作时候，也是具有比较好的cache局部性的。

引申思考:

不同的数据排布性能不同，那么对于具体一个硬件平台，是否可以先确定哪种数据排布更快，在算子计算前转换成更快的数据排布格式呢？或者说对于一个网络的不同算子，不同的数据排布对于算子影响不同，那么能不能对于网络中不同算子，使用不同的数据排布格式，也就是说，整个网络图中，数据流从头到尾，不只是一种数据排布格式。初步调研了一下，有类似的方案借鉴: https://zhuanlan.zhihu.com/p/491037155

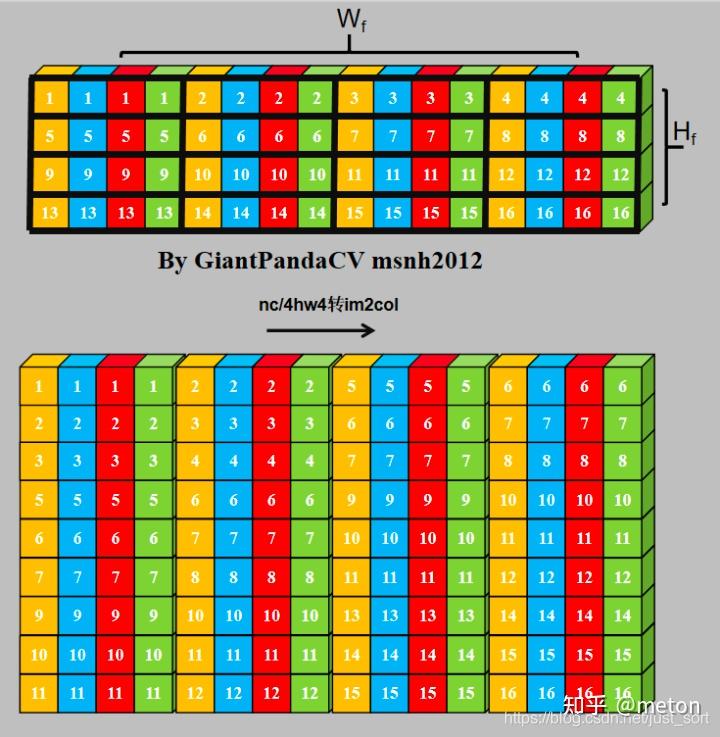
当使用NC4HWc4结合GEMM，好处在于：

对于内部的HWc4小块，使用GEMM时候，通过对卷积权重离线数据重排，整体AB矩阵运算时候对于cache更加友好(参考NCHW和NHWC内存排布对GEMM性能影响那一小节)。
对于外部NC4，其实便于使用多线编程，使用N*C4个线程去分别计算内循环中的HWc4小块的GEMM运算。更好地利用CPU多核多线程能力。

总结：

原始卷积操作可以通过im2col转化为GEMM操作。
GEMM操作可以通过传统矩阵优化技术如分块来提高访存操作的Cache友好性。Cache友好性之所以那么重要是由于现有架构中从DRAM取数时钟周期远远大于计算指令执行周期这一低层约束所决定的。
矩阵分块在代码实现是将原本最naive的三层循环实现进行分成多层循环，降低可读性，提高性能。
混合排布NC4HW4兼具NHWC比NCHW优点（访存友好+结合多线程并行）。

1969年，Volker Strassen提出了第一个算法时间复杂度低于 Θ(N3) 矩阵乘法算法，算法复杂度为 Θ(nlog27)=Θ(n2.807) 。从下图可知，Strassen算法只有在对于维数比较大的矩阵 (N>300) ，性能上才有很大的优势，可以减少很多乘法计算。

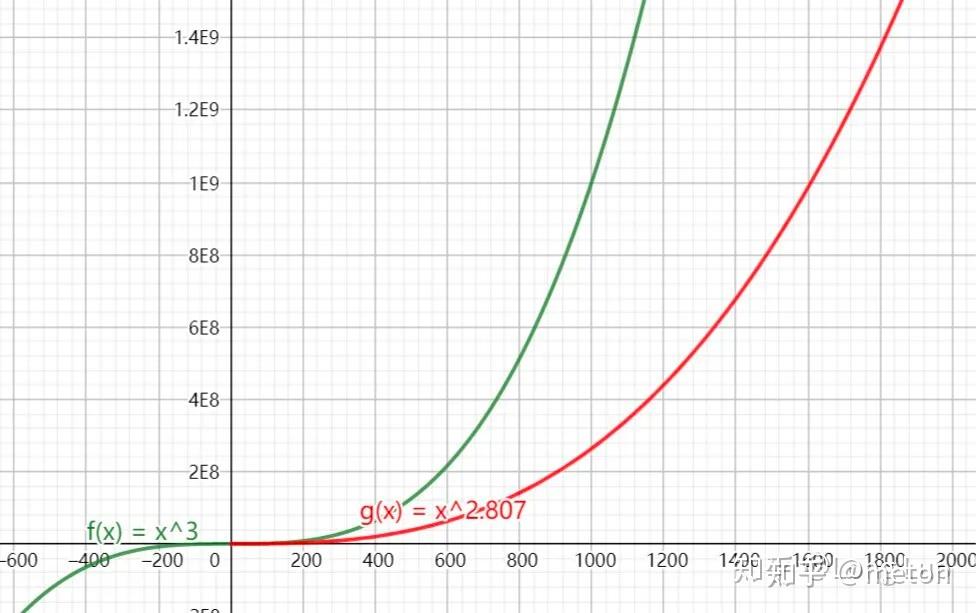
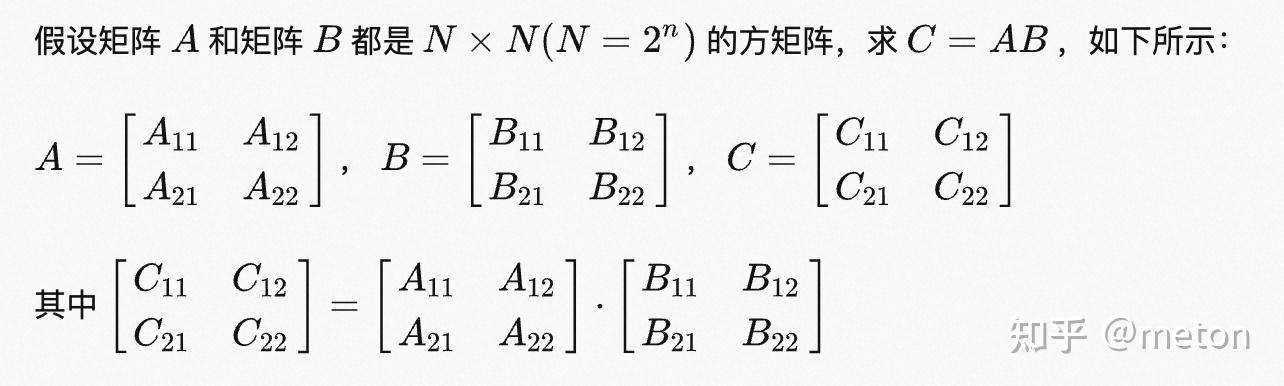
一般我们实现卷积的时候大多采用的方案是im2col+gemm, 除此之外, 还有一种加速方案, 就是Winograd卷积, 目前几乎在所有推理框架里都能找到其实现. Winograd卷积出自一篇2016CVPR论文.

Winograd的核心思想就是通过增加加法操作来减少乘法操作从而实现计算加速。

Winograd本身是建立在GEMM转化之上的，下图表示对于一个输入和卷积核，输入通过im2col进行转化，而卷积核参数则转换为9*1向量。

对矩阵进行划分，转化为右图矩阵与向量的运算形式。

进行公式计算，可以算得结果矩阵M，而M0、M1、M2、M3公式中，W相关的系数都是由卷积参数计算得到的，这部分的计算可以在离线进行计算，变成常数系数。
这样就将原本9次乘法+4次加法，变成了4次乘法+4次加减法。达到节省乘法次数的效果。
注意，这里的K0~K3，W0~W2，M0~M3其实都是子矩阵，而他们计算模式也是矩阵*向量模式，因此也是符合上述的计算的，因此其实还蕴含一层内层的Wingrad计算，对于M0~M3，进行Wingrad类似的推导过程，如下图所示:

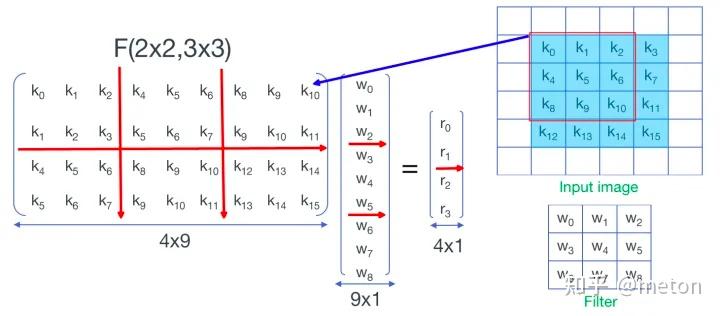
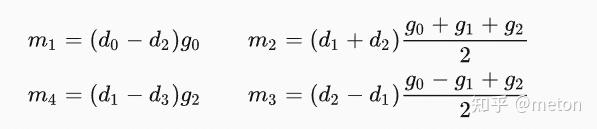
总体来看，wingrad卷积可以分成两步：

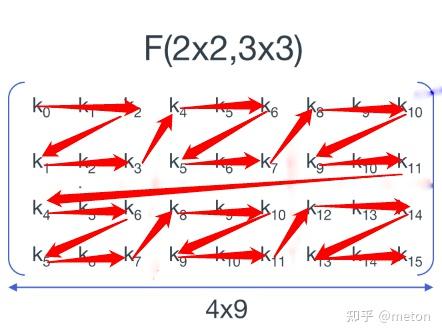
输入的im2col处理和权重向量排布，注意为了Cache友好性，可以进行对矩阵进行数据重排。

进行嵌套的两层wingrad计算:

Winograd的几个字母表示的含义. 上面我们一直讲的都是Winograd的, 这里2对应的是, 代表输出的尺寸为2x2, 3对应的是, 代表卷积核的尺寸为3x3. 我们的输入尺寸为4x4, 叫做tile块, 用来表示tile的尺寸.

如果我们输入是更大的比如[8, 8]应该如何处理呢? 答案就是切块, 把输入切成多个tile块, 每个tile都单独进行上述的计算即可. 在切块的时候我们需要注意相邻tile是有重叠的, 重叠的大小为. 示意图如下:

卷积通过im2col可以变成矩阵x向量的形式。
矩阵x向量，从理解上，可以拆解成两层wingard的推导过程。
通过系数离线计算，其实可以将在线计算部分的乘法次数缩减。
卷积的stride等于2时加速收益不高。
深度可分离卷积用Winograd不划算。
Winograd卷积由于一些系数是是除不尽的, 所以有一定的精度损失。
tile块越大, 加速效果越好。

稀疏矩阵乘法是指在矩阵乘法中，其中一个或两个矩阵是稀疏矩阵（大部分元素为零），从而可以减少计算量和存储空间的使用，提高计算效率。具体来说，稀疏矩阵乘法可以通过以下步骤实现：

算法端：

1. 算法侧可能需要进行稀疏训练，是的模型参数都是稀疏的。模型参数可以看做一系列稀疏矩阵。

2. 也可以不进行稀疏训练，算法侧得到稠密参数后，利用离线细粒度剪枝，对网络进行细粒度结构化稀疏，再使用学习率重卷 (learning rate rewinding) 的方式对网络进行微调。

推理端：

对稀疏矩阵进行压缩，即去除其中的零元素，并记录下每个非零元素的位置index和值value，这样可以结束存储空间。
对压缩后的稀疏矩阵和另一个矩阵进行乘法计算，只对非零位置进行计算，并将结果存储在一个新的矩阵中。
最后，将结果中的非零元素重新还原到稀疏矩阵的位置上，并填充零元素。

稀疏矩阵乘法在实际应用中非常重要，特别是在机器学习和深度学习中，因为矩阵乘法在神经网络中是非常常见的运算。通过使用稀疏矩阵乘法，可以大幅度提高计算效率和模型的运行速度。

如果硬件本身支持稀疏计算，那么稀疏计算可以更加高效，例如A100:

https://zhuanlan.zhihu.com/p/148211855

卷积傅里叶变换的思想来自于数字信号处理领域:

也就是时间域上的卷积操作可以变成频域空间中的乘法操作(牛逼思想)。傅里叶变换在数字信号处理中应用非常广泛。在深度学习中的卷积，傅里叶变换似乎不太常用，因为要达到理论上的加速，要求*大卷积核*才可以，而实际上深度学习用的都是小卷积核,其性能优势远没有其他优化方法明显,在这里不详细学习。

不过最近出现了一种超大卷积核的文艺复兴, 最大使用了31X31的卷积核，感兴趣可以关注！

对量化的几个认知：

1.为什么量化有用？

CNN对噪声不敏感。

2. 为什么用量化？

模型太大，比如alexnet就200MB，量化后减少模型flash或者磁盘存储大小
每个层的weights范围基本都是确定的，且波动不大，适合量化压缩。
量化的好处是双份的：减少访存又减少计算量。

3.卷积量化的优势

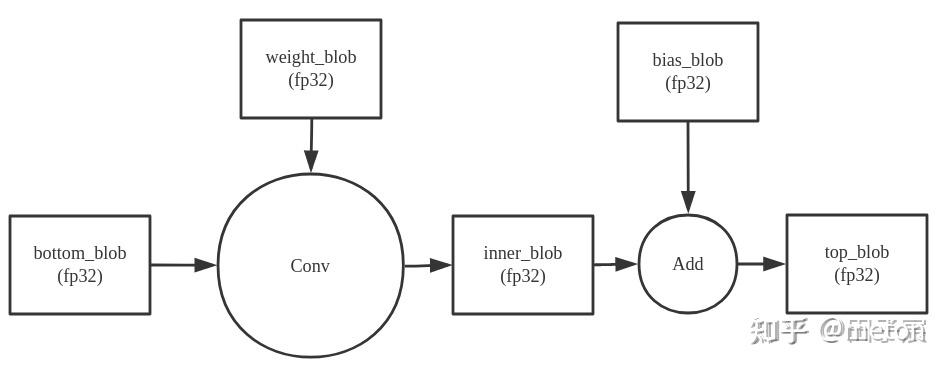
卷积计算占据了绝大多数网络的运算量，对卷积进行INT8量化收益高。

正常的fp32计算中，一个Conv的计算流程如下：

在NCNN Conv进行Int8计算时，计算流程如下：

NCNN首先将输入(bottom_blob)和权重(weight_blob)量化成INT8，在INT8下计算卷积，然后反量化到fp32，再和未量化的bias相加，得到输出(top_blob)。

输入和权重的量化公式：

bottom_blob(int8)=bottom_blob_int8_scale?bottom_blob(fp32) weight_blob(int8)=weight_data_int8_scale?weight_blob(fp32)

反量化的目的是将int8映射回原来的fp32，范围要保持一致；由于weight_blob(int8)和bottom_blob(int8)是相乘的：

inner_blob(int32)=(bottom_blob_int8_scale?weight_data_int8_scale)?(bottom_blob(fp32)?weight_blob(fp32))

所以为了实现一个反映射，量化反量化的scale应该为：

dequantize_scale=1/(bottom_blob_int8_scale?weight_data_int8_scale)

inner_blob(fp32)=dequantize_scale?inner_blob(int32)

NCNN并没有对bias做量化。另外值得一提的是，由于权重不会变，权重是在网络初始化时量化的；而输入由于会变化，是在线量化的。

当一个Conv1后面紧跟着另一个Conv2时，NCNN会进行requantize的操作。大致意思就是在得到Conv1的INT32输出后，会顺手帮Conv2做量化，得到Conv2的INT8输入。这中间不会输出fp32的blob，节省一次内存读写

原来的流程中（上图），第一个Conv计算完int32后，会使用scale=1/(s1*s2)进行反量化，然后加上bias，得到fp32的输出。之后再在下一层使用s3进行量化。
而requantize将反量化、加bias、量化的过程合起来，直接得到下一层Conv的int8输入，可以节省一次fp32数据的读写。

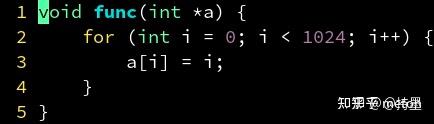
单个指令处理多个数据的技术称为 SIMD（single-instruction multiple-data）。他可以大大增加计算密集型程序的吞吐量。因为 SIMD 把 4 个 float 打包到一个 xmm 寄存器里同时运算，很像数学中矢量的逐元素加法。因此 SIMD 又被称为矢量，而原始的一次只能处理 1 个 float 的方式，则称为标量。在一定条件下，编译器能够把一个处理标量 float 的代码，转换成一个利用 SIMD 指令的，处理矢量 float 的代码，从而增强你程序的吞吐能力。通常认为利用同时处理 4 个 float 的 SIMD 指令可以加速 4 倍。但是如果你的算法不适合 SIMD，则可能加速达不到 4 倍；也有因为 SIMD 让访问内存更有规律，节约了指令解码和指令缓存的压力等原因，出现加速超过 4 倍的情况。目前要利用SIMD去加速卷积主要有如下几种:

自动向量化:

现代编译器支持，由编译器分析循环代码内层，并根据硬件平台将代码替换成向量指令，但是编译器的这种自动向量化一般比较保守, 可能生成不了性能较好的向量代码，可能有负优化，毕竟编译器只有离线信息可以利用。

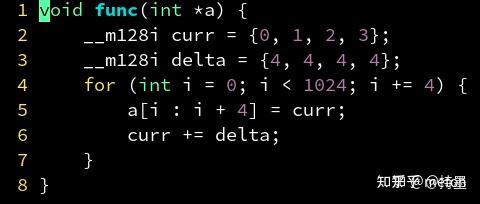
手写汇编，一般只手写性能瓶颈的kernel代码，需要对硬件和体系结构有深刻了解。

下面展示的是 Paddle-lite的conv3x3s1px_depthwise_fp32实现中的部分汇编代码:

#define COMPUTE \\
          /* load weights */ \\
          "vld1.32{d10-d13},[%[wc0]]!      @ load w0, w1, to q5, q6\
" \\
          "vld1.32{d14-d15},[%[wc0]]!      @ load w2, to q7\
" \\
          /* load r0, r1 */ \\
          "vld1.32{d0-d3},[%[r0]]!         @ load r0, q0, q1\
" \\
          "vld1.32{d4-d7},[%[r0]]!         @ load r0, q2, q3\
" \\
          /* main loop */ \\
          "0:                                   @ main loop\
" \\
          /* mul r0 with w0, w1, w2, get out r0 */ \\
          "vmul.f32   q8, q5, q0                @ w0 * inr00\
" \\
          "vmul.f32   q9, q5, q1                @ w0 * inr01\
" \\
          "vmul.f32   q10, q5, q2               @ w0 * inr02\
" \\
          "vmul.f32   q11, q5, q3               @ w0 * inr03\
" \\
          "vmla.f32   q8, q6, q1                @ w1 * inr01\
" \\
          "vld1.32{d0-d3},[%[r0]]@ load r0, q0, q1\
" \\
          "vmla.f32   q9, q6, q2                @ w1 * inr02\
" \\
          "vmla.f32   q10, q6, q3               @ w1 * inr03\
" \\
          "vmla.f32   q11, q6, q0               @ w1 * inr04\
" \\
          "vmla.f32   q8, q7, q2                @ w2 * inr02\
" \\
          "vmla.f32   q9, q7, q3                @ w2 * inr03\
" \\
          "vld1.32{d4-d7},[%[r1]]!         @ load r0, q2, q3\
" \\
          "vmla.f32   q10, q7, q0               @ w2 * inr04\
" \\
          "vmla.f32   q11, q7, q1               @ w2 * inr05\
" \\
          "vld1.32{d0-d3},[%[r1]]!         @ load r0, q0, q1\
" \\
          "vld1.32{d8-d9},[%[wc0]]!        @ load w3 to q4\
" \\
          /* mul r1 with w0-w5, get out r0, r1 */ \\
          "vmul.f32   q12, q5, q2               @ w0 * inr10\
" \\
          "vmul.f32   q13, q5, q3               @ w0 * inr11\
" \\
          "vmul.f32   q14, q5, q0               @ w0 * inr12\
" \\
          "vmul.f32   q15, q5, q1               @ w0 * inr13\
" \\
          "vld1.32{d10-d11},[%[wc0]]!      @ load w4 to q5\
" \\
          "vmla.f32   q8, q4, q2                @ w3 * inr10\
" \\
          "vmla.f32   q9, q4, q3                @ w3 * inr11\
" \\
          "vmla.f32   q10, q4, q0               @ w3 * inr12\
" \\
          "vmla.f32   q11, q4, q1               @ w3 * inr13\
" \\
          /* mul r1 with w1, w4, get out r1, r0 */ \\
          "vmla.f32   q8, q5, q3                @ w4 * inr11\
" \\
          "vmla.f32   q12, q6, q3               @ w1 * inr11\
" \\
          "vld1.32{d4-d7},[%[r1]]@ load r1, q2, q3\
" \\
          "vmla.f32   q9, q5, q0                @ w4 * inr12\
" \\
          "vmla.f32   q13, q6, q0               @ w1 * inr12\
" \\
          "vmla.f32   q10, q5, q1               @ w4 * inr13\
" \\
          "vmla.f32   q14, q6, q1               @ w1 * inr13\
" \\
          "vmla.f32   q11, q5, q2               @ w4 * inr14\
" \\
          "vmla.f32   q15, q6, q2               @ w1 * inr14\
" \\
          "vld1.32{d12-d13},[%[wc0]]!      @ load w5 to q6\
" \\
          /* mul r1 with w2, w5, get out r1, r0 */ \\
          "vmla.f32   q12, q7, q0               @ w2 * inr12\
" \\
          "vmla.f32   q13, q7, q1               @ w2 * inr13\
" \\
          "vmla.f32   q8, q6, q0                @ w5 * inr12\
" \\
          "vmla.f32   q9, q6, q1                @ w5 * inr13\
" \\
          "vld1.32{d0-d3},[%[r2]]!         @ load r2, q0, q1\
" \\
          "vmla.f32   q14, q7, q2               @ w2 * inr14\
" \\
          "vmla.f32   q15, q7, q3               @ w2 * inr15\
" \\
          "vmla.f32   q10, q6, q2               @ w5 * inr14\
" \\
          "vmla.f32   q11, q6, q3               @ w5 * inr15\
" \\
          "vld1.32{d4-d7},[%[r2]]!         @ load r2, q0, q1\
" \\
          "vld1.32{d14-d15},[%[wc0]]!      @ load w6, to q7\
" \\
          /* mul r2 with w3-w8, get out r0, r1 */ \\
          "vmla.f32   q12, q4, q0               @ w3 * inr20\
" \\
          "vmla.f32   q13, q4, q1               @ w3 * inr21\
" \\
          "vmla.f32   q14, q4, q2               @ w3 * inr22\
" \\
          "vmla.f32   q15, q4, q3               @ w3 * inr23\
" \\
          "vld1.32{d8-d9},[%[wc0]]!        @ load w7, to q4\
" \\
          "vmla.f32   q8,  q7, q0               @ w6 * inr20\
" \\
          "vmla.f32   q9,  q7, q1               @ w6 * inr21\
" \\
          "vmla.f32   q10, q7, q2               @ w6 * inr22\
" \\
          "vmla.f32   q11, q7, q3               @ w6 * inr23\
" \\
          /* mul r2 with w4, w7, get out r1, r0 */ \\
          "vmla.f32   q8,  q4, q1               @ w7 * inr21\
" \\
          "vmla.f32   q12, q5, q1               @ w4 * inr21\
" \\
          "vld1.32{d0-d3},[%[r2]]@ load r2, q0, q1\
" \\
          "vmla.f32   q9,  q4, q2               @ w7 * inr22\
" \\
          "vmla.f32   q13, q5, q2               @ w4 * inr22\
" \\
          "vmla.f32   q10, q4, q3               @ w7 * inr23\
" \\
          "vmla.f32   q14, q5, q3               @ w4 * inr23\
" \\
          "vmla.f32   q11, q4, q0               @ w7 * inr24\
" \\
          "vmla.f32   q15, q5, q0               @ w4 * inr24\
" \\
          "vld1.32{d10-d11},[%[wc0]]!      @ load w8 to q5\
" \\
          /* mul r1 with w5, w8, get out r1, r0 */ \\
          "vmla.f32   q12, q6, q2               @ w5 * inr22\
" \\
          "vmla.f32   q13, q6, q3               @ w5 * inr23\
" \\
          "vmla.f32   q8,  q5, q2               @ w8 * inr22\
" \\
          "vmla.f32   q9,  q5, q3               @ w8 * inr23\
" \\
          "vld1.32{d4-d7},[%[r3]]!         @ load r3, q2, q3\
" \\
          "ldr r4,[%[outl], #32]@ load bias addr to r4\
" \\
          "vmla.f32   q14, q6, q0               @ w5 * inr24\
" \\
          "vmla.f32   q15, q6, q1               @ w5 * inr25\
" \\
          "vmla.f32   q10, q5, q0               @ w8 * inr24\
" \\
          "vmla.f32   q11, q5, q1               @ w8 * inr25\
" \\
          "vld1.32{d0-d3},[%[r3]]!         @ load r3, q0, q1\
" \\
          "sub %[wc0], %[wc0], #144      @ wc0 - 144 to start address\
" \\
          /* mul r3 with w6, w7, w8, get out r1 */ \\
          "vmla.f32   q12, q7, q2               @ w6 * inr30\
" \\
          "vmla.f32   q13, q7, q3               @ w6 * inr31\
" \\
          "vmla.f32   q14, q7, q0               @ w6 * inr32\
" \\
          "vmla.f32   q15, q7, q1               @ w6 * inr33\
" \\
          "vmla.f32   q12, q4, q3               @ w7 * inr31\
" \\
          "vld1.32{d4-d7},[%[r3]]@ load r3, q2, q3\
" \\
          "vld1.32{d12-d13},[r4]@ load bias\
" \\
          "vmla.f32   q13, q4, q0               @ w7 * inr32\
" \\
          "vmla.f32   q14, q4, q1               @ w7 * inr33\
" \\
          "vmla.f32   q15, q4, q2               @ w7 * inr34\
" \\
          "ldr r0,[%[outl]]@ load outc00 to r0\
" \\
          "vmla.f32   q12, q5, q0               @ w8 * inr32\
" \\
          "vmla.f32   q13, q5, q1               @ w8 * inr33\
" \\
          "vmla.f32   q14, q5, q2               @ w8 * inr34\
" \\
          "vmla.f32   q15, q5, q3               @ w8 * inr35\
" \\
          "ldr r1,[%[outl], #4]@ load outc10 to r1\
" \\
          "vadd.f32   q8, q8, q6                @ r00 add bias\
" \\
          "vadd.f32   q9, q9, q6                @ r01 add bias\
" \\
          "vadd.f32   q10, q10, q6              @ r02 add bias\
" \\
          "vadd.f32   q11, q11, q6              @ r03 add bias\
" \\
          "ldr r2,[%[outl], #8]@ load outc20 to r2\
" \\
          "vadd.f32   q12, q12, q6              @ r10 add bias\
" \\
          "vadd.f32   q13, q13, q6              @ r11 add bias\
" \\
          "vadd.f32   q14, q14, q6              @ r12 add bias\
" \\
          "vadd.f32   q15, q15, q6              @ r13 add bias\
" \\
          "ldr r3,[%[outl], #12]@ load outc30 to r3\
" \\
          "vmov.u32   q7, #0                    @ mov zero to q7\
"

https://zhuanlan.zhihu.com/p/428014053

https://hanlab.mit.edu/projects/tinyml/mcunet/

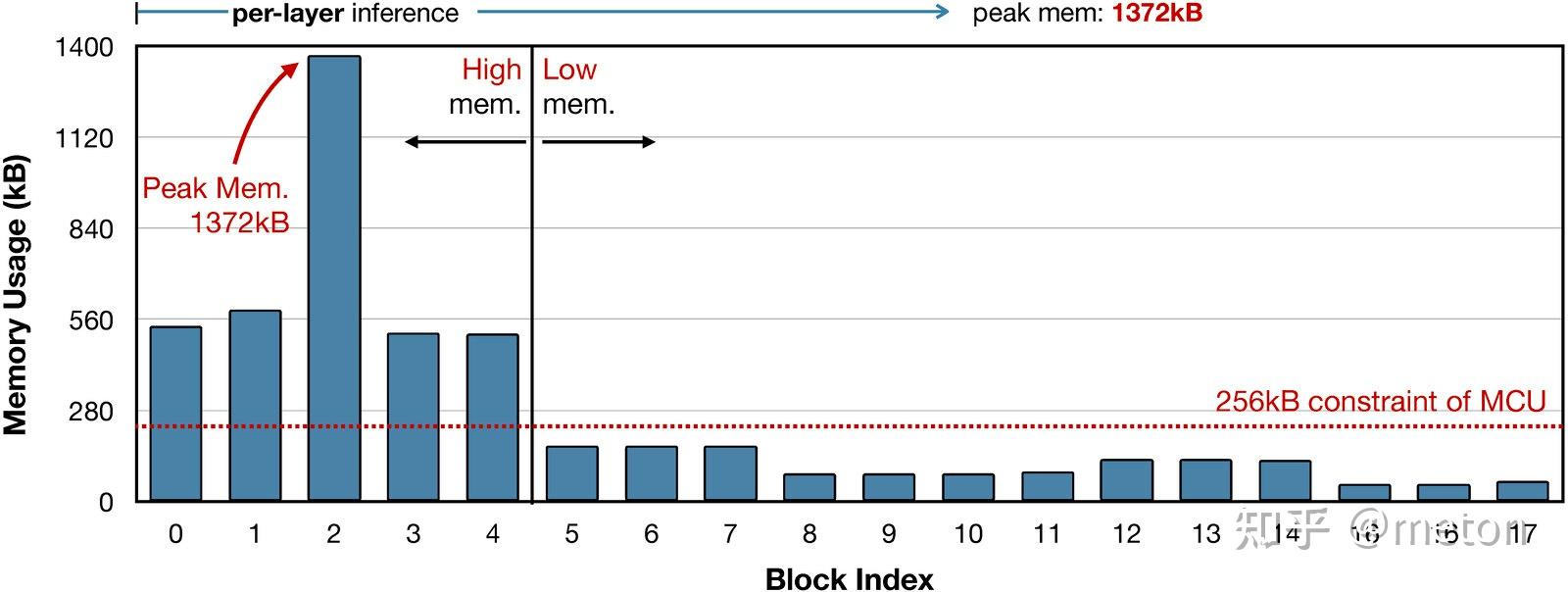
Imbalanced memory distribution 问题:

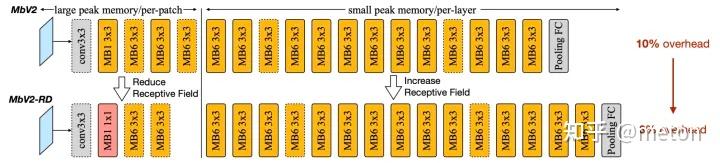
以MobileNetV2为例，上图提供了每个模块的峰值峰值内存占用(注：上述信息通过int8度量得到)。我们可看到非常清晰的内存占用分布不平衡：前5个模块具有非常大的峰值内存，超出了MCUs内存约束，而其他13个模块则能轻易满足256kB内存约束 。我们同样检查了其他高效网络架构(包含针对MCU而设计的MCUNet)并发现了类似的现象。论文发现：该现象适用于大部分单分支与残差CNN架构。每个阶段，图像分类率降低一半，通道数仅乘2，故特征尺寸逐渐减小。因此，内存瓶颈倾向于出现在网络的早期阶段 。

这种内存分布不平衡问题极大限制了MCU端的模型容量与输入分辨率。为适应初始阶段内存密集问题，整个网络都需要进行缩小，哪怕大部分网络已经具有非常小的内存占用。这也就使得分辨率敏感的任务(如目标检测)难以落地MCU端。以MobileNetV2的第一个卷积为例，输入通道为3，输出通道维32，stride=2，当输入图像分辨率为224×224 时需要占用的内存为3×2242+32×1122=539kB3 (注：int8量化)，这是当前MCU所无法满足的。另一方面，如果我们能找到一种方式跳过内存密集阶段，我们就可以大幅降低整个网络的峰值内存，进而有了更大的优化空间。

现有的推理框架(如TFLite Micro, TinyEngine, MicroTVM)采用layer-by-layer方式运行。对于每个卷积层，推理库首先在SRAM中开辟输入与输出buffer，完成计算后释放输入buffer。这种处理机制更易于进行推理优化(比如im2col, tiling)，但是SRAM必须保留完整的输入与输出buffer。

patch-based inference 机制打破初始层的内存瓶颈问题，见下图。本文所提patch-based推理则在内存密集阶段以patch-by-patch方式运行 (见下图右)。模型每次仅在小比例区域(比完整区域小10倍)进行计算，这可以有效降低峰值内存占用。当完成该部分后，网络的其他具有较小峰值内存的模块则采用常规的layer-by-layer 方式运行。

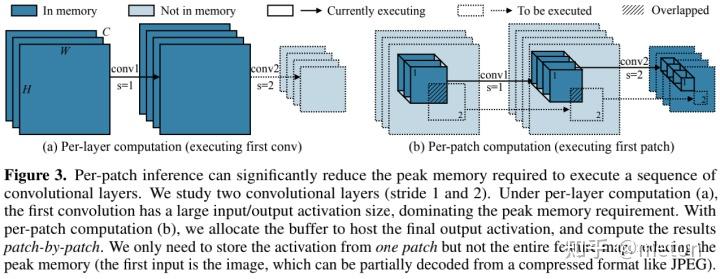
以上图stride=1/2的图示为例，对于逐层计算方式，第一层具有大输入输出尺寸，导致非常高内存占用。通过空域拆分计算，我们以patch-by-patch方式开辟buffer并进行计算，此时我们仅需保存一个块的buffer而非完整特征图。Computation overhead 内存节省的代价来自计算负载提升。为与逐层推理相同的输出结果，非重叠输出块需要对应了重叠输入块(见上图b阴影区域)。这种重复性的计算会提升网络整体10-17%计算量，这是低功耗边缘设备所不期望的。

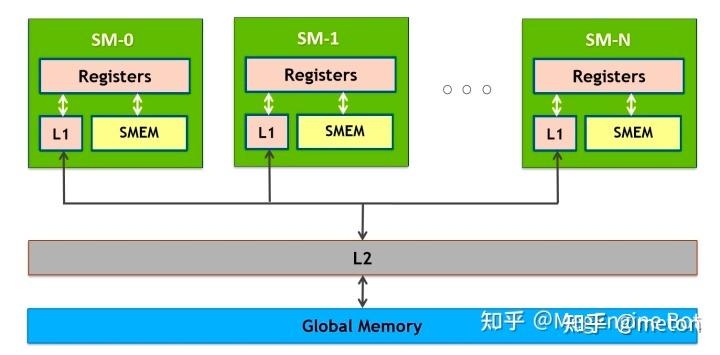
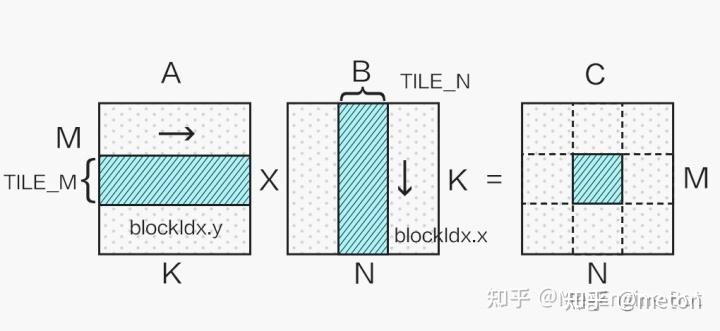
本质上patch-by-patch推理并没有改变卷积原本的计算方式，而是对输入tensor进行空域拆分，相当于每次只在内存中处理一小块data patch的卷积计算，从而节省整个网络的内存峰值。
patch-by-pacth推理主要是要剖视网络推理，找到内存峰值的layer。

GPU使用的是SIMT加速，软件编程抽象是 grid-block-thread。对于输出矩阵C，切分成grid,网格。每个网格是一个block, 每个block分配若干线程去计算，每个线程计算小部分结果。各个block之间的计算是并发执行，充分利用GPU的SM。

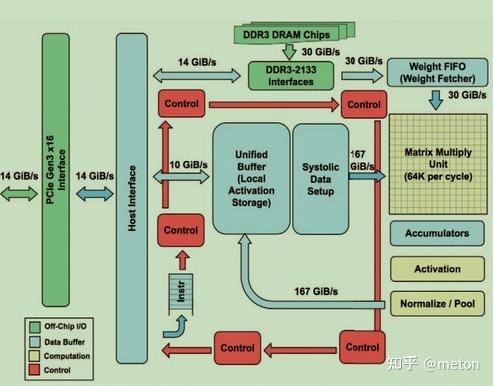
TPU核心单元是脉动阵列

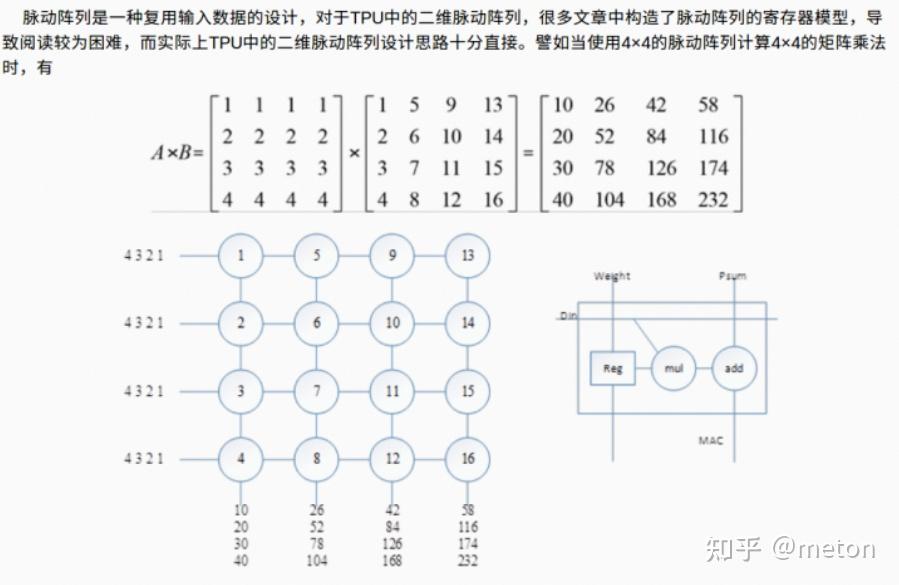
简述一下脉动阵列计算方式：

权重先送进各个PE，之后input 矩阵数据从左往右流进阵列计算
之后计算结果从下面依次流出（不同列输出相差若干个周期），类似数据流架构，但是更加专用。

脉动矩阵的设计哲学：

Simple and regular design：可以说，简单和规则是脉动阵列的一个重要原则。而这样的设计主要是从“成本”的角度来考虑问题的。
Balancing computation with I/O：平衡运算和I/O，应该说是脉动阵列最重要的设计目标。尽量让数据在运算部件中多停留。尽量让运算部件保持繁忙，不会因为要取数而停滞计算。

inline void HybridConvPerChannel(
    const ConvParams& params, float* scaling_factors_ptr,
    const RuntimeShape& input_shape, const int8_t* input_data,
    const RuntimeShape& filter_shape, const int8_t* filter_data,
    const RuntimeShape& bias_shape, const float* bias_data,
    const RuntimeShape& output_shape, float* output_data,
    const RuntimeShape& im2col_shape, int8_t* im2col_data,
    const float* per_channel_scale, int32_t* input_offset){
  (void)im2col_data;   // only used in optimized code.
  (void)im2col_shape;  // only used in optimized code.
  const int stride_width=params.stride_width;
  const int stride_height=params.stride_height;
  const int dilation_width_factor=params.dilation_width_factor;
  const int dilation_height_factor=params.dilation_height_factor;
  const int pad_width=params.padding_values.width;
  const int pad_height=params.padding_values.height;
  const float output_activation_min=params.float_activation_min;
  const float output_activation_max=params.float_activation_max;
  TFLITE_DCHECK_EQ(input_shape.DimensionsCount(), 4);
  TFLITE_DCHECK_EQ(filter_shape.DimensionsCount(), 4);
  TFLITE_DCHECK_EQ(output_shape.DimensionsCount(), 4);
  const int batches=MatchingDim(input_shape, 0, output_shape, 0);
  const int input_depth=input_shape.Dims(3);
  const int output_depth=MatchingDim(filter_shape, 0, output_shape, 3);
  if (bias_data){
    TFLITE_DCHECK_EQ(bias_shape.FlatSize(), output_depth);
  }
  const int input_height=input_shape.Dims(1);
  const int input_width=input_shape.Dims(2);
  const int filter_height=filter_shape.Dims(1);
  const int filter_width=filter_shape.Dims(2);
  const int filter_input_depth=filter_shape.Dims(3);
  const int groups=input_depth / filter_input_depth;
  TFLITE_DCHECK_EQ(input_depth % filter_input_depth, 0);
  const int filters_per_group=output_depth / groups;
  const int output_height=output_shape.Dims(1);
  const int output_width=output_shape.Dims(2);

  //核心7层循环
  //外层循环是从输出tensor的每个点开始
  for (int batch=0; batch < batches; ++batch){
    for (int out_y=0; out_y < output_height; ++out_y){
      for (int out_x=0; out_x < output_width; ++out_x){
        //nhwc排布，所以是channel最后遍历，channel维度的元素是连续存储的
        for (int out_channel=0; out_channel < output_depth; ++out_channel){
            
          auto group=out_channel / filters_per_group;
          //从输出tensor的某个点计算映射回卷积输入tensor对应的左上角坐标
          const int in_x_origin=(out_x * stride_width) - pad_width;
          const int in_y_origin=(out_y * stride_height) - pad_height;
          int32_t acc=0;

          //内层遍历卷积核，取卷积核3*3每个位置对应通道的所有元素去做卷积运算
          for (int filter_y=0; filter_y < filter_height; ++filter_y){
            for (int filter_x=0; filter_x < filter_width; ++filter_x){
              for (int in_channel=0; in_channel < filter_input_depth;
                   ++in_channel){
                //考虑膨胀卷积情况，此时需要参与卷积的原图点坐标发生变化
                const int in_x=in_x_origin + dilation_width_factor * filter_x;
                const int in_y=            in_y_origin + dilation_height_factor * filter_y;
                // If the location is outside the bounds of the input image,
                // use zero as a default value.
                if ((in_x >=0) && (in_x < input_width) && (in_y >=0) &&
                    (in_y < input_height)){
                  int32_t input_val=input_data[Offset(
                      input_shape, batch, in_y, in_x,
                      in_channel + group * filter_input_depth)];
                  int32_t filter_val=              filter_data[Offset(filter_shape, out_channel, filter_y,
                                         filter_x, in_channel)];
                  //int8运算后结果存在int32
                  acc +=filter_val * (input_val - input_offset[batch]);
                }
              }
            }
          }
          //dequant操作
          float acc_float=      acc * per_channel_scale[out_channel]* scaling_factors_ptr[batch];
          if (bias_data){
            acc_float +=bias_data[out_channel];
          }
          //激活
          output_data[Offset(output_shape, batch, out_y, out_x, out_channel)]=      ActivationFunctionWithMinMax(acc_float, output_activation_min,
                                           output_activation_max);
        }
      }
    }
  }
}

总结：

tflitemicro的卷积其实使用的是最朴素的多层循环实现，这里没有使用im2col的优化，而是直接的卷积运算，代码非常好懂。

NCNN 深度卷积和组卷积是一种实现，深度卷积是组卷积的一种 inch==group && group==outch 的特殊情况，阅读代码时结合下面两幅图便非常好懂。左图是深度卷积，右图是组卷积。

static int convolutiondepthwise(const Mat& bottom_blob, Mat& top_blob, const Mat& weight_data, const Mat& bias_data, int kernel_w, int kernel_h, int stride_w, int stride_h, int dilation_w, int dilation_h, int group, int activation_type, const Mat& activation_params, const Option& opt)
{
    const int w=bottom_blob.w;
    const int inch=bottom_blob.c;

    const int outw=top_blob.w;
    const int outh=top_blob.h;
    const int outch=top_blob.c;

    const int bias_term=bias_data.empty() ? 0 : 1;

    const int maxk=kernel_w * kernel_h;

    // kernel offsets
    // 创建一个大小为 maxk 的整型数组 _space_ofs，用于存储卷积核在输入数据中的偏移量
    // 将偏移量计算相当于一个计算模板，每次卷积操作都需要用到，
    // 所以在卷积计算前开始先一次性计算好，并存储起来
    std::vector<int> _space_ofs(maxk);
    int* space_ofs=&_space_ofs[0];
{
        int p1=0;
        int p2=0;
        int gap=w * dilation_h - kernel_w * dilation_w;
        for (int i=0; i < kernel_h; i++)
{
            for (int j=0; j < kernel_w; j++)
{
                space_ofs[p1]=p2;
                p1++;
                p2 +=dilation_w;
            }
            p2 +=gap;
        }
    }

    // NCNN 深度卷积和组卷积是一种实现，
    // 深度卷积是组卷积的一种 inch==group && group==outch 的特殊情况
    // depth-wise
    if (inch==group && group==outch)
{
        #pragma omp parallel for num_threads(opt.num_threads)
        for (int g=0; g < group; g++) // 外循环，输出channel是 group数
{
            float* outptr=top_blob.channel(g);
            // 选中卷积参数中某一个group的数据起始偏移
            const float* kptr=(const float*)weight_data + maxk * g;
            const Mat m=bottom_blob.channel(g);

            //中层两循环，计算output tensor一个平面的结果
            for (int i=0; i < outh; i++) 
{
                for (int j=0; j < outw; j++)
{
                    float sum=0.f;

                    if (bias_term)
                        sum=bias_data[g];
                	// 从输出点(i，j)倒推它在输入tensor m中的开始位置
                    const float* sptr=m.row(i * stride_h) + j * stride_w;

                    //内层循环， 遍历kernel元素
                    for (int k=0; k < maxk; k++)
{
                        //根据前面计算好的偏移模板space_ofs，选中对应的元素
                        float val=sptr[space_ofs[k]];
                        float w=kptr[k];
                        // 核心计算，乘累加，卷积原理其实就这一行
                        sum +=val * w;
                    }
                	// 激活函数
                    outptr[j]=activation_ss(sum, activation_type, activation_params);
                }

                outptr +=outw;
            }
        }
    }
    else
{
        // group convolution
        const int inch_g=inch / group; //计算输入tensor每一组有inch_g通道数的数据
        const int outch_g=outch / group; 

#ifdef _WIN32
        #pragma omp parallel for num_threads(opt.num_threads)
#else
        #pragma omp parallel for collapse(2) num_threads(opt.num_threads)
#endif
        for (int g=0; g < group; g++) //多少组
{
            for (int p=0; p < outch_g; p++) // 输出tensor分多少outch_g 来产生
{
                // 选择一个channel
                float* outptr=top_blob.channel(g * outch_g + p);
                const float* weight_data_ptr=(const float*)weight_data + maxk * inch_g * outch_g * g;

                // shadowed variable for less openmp task args
                const int outw=top_blob.w;
                const int outh=top_blob.h;

                for (int i=0; i < outh; i++)
{
                    for (int j=0; j < outw; j++)
{
                        float sum=0.f;

                        if (bias_term)
                            sum=bias_data[outch_g * g + p];

                        const float* kptr=weight_data_ptr + maxk * inch_g * p;

                        for (int q=0; q < inch_g; q++)
{
                            const Mat m=bottom_blob.channel(inch_g * g + q);
                            const float* sptr=m.row(i * stride_h) + j * stride_w;

                            for (int k=0; k < maxk; k++)
{
                                float val=sptr[space_ofs[k]];
                                float w=kptr[k];
                                sum +=val * w;
                            }

                            kptr +=maxk;
                        }

                        outptr[j]=activation_ss(sum, activation_type, activation_params);
                    }

                    outptr +=outw;
                }
            }
        }
    }

    return 0;
}

在ARM平台中，深度卷积int8模式的通用SIMD代码中，核心卷积计算逻辑变成，即利用了硬件向量化能力。

向量取数 + 向量MUL + 向量规约(reduce, 累加)

for (int k=0; k < maxk; k++)
{
    int8x8_t _val=vld1_s8(sptr + space_ofs[k]* 8);
    int8x8_t _w=vld1_s8(kptr + k * 8);
    int16x8_t _s0=vmull_s8(_val, _w);
    _sum0=vaddw_s16(_sum0, vget_low_s16(_s0));
    _sum1=vaddw_s16(_sum1, vget_high_s16(_s0));
}

在ARM平台中，对于特殊情况(常见的stride 1 stride 2等 )的卷积，会使用专门的优化实现(手写调优算子)

if (elempack==8)
{
    if (kernel_w==3 && kernel_h==3 && dilation_w==1 && dilation_h==1 && stride_w==1 && stride_h==1 && (activation_type==0 || activation_type==1))
{
        ....
        convdw3x3s1_pack8_int8_neon(bottom_blob_bordered, top_blob_int32, \\
            weight_data_tm, opt);
        ....
    }
    else if (kernel_w==3 && kernel_h==3 && dilation_w==1 && dilation_h==1 && stride_w==2 && stride_h==2 && (activation_type==0 || activation_type==1))
{
        ...
        convdw3x3s2_pack8_int8_neon(bottom_blob_bordered, \\
            top_blob_int32, weight_data_tm, opt);
...
 ...
   ...

以convdw3x3s1_pack8_int8_neon()为例:

在SIMD的加持下，相当于在一个循环体中，尽可能多排几个计算操作，这样连续计算出多个结果。这种叫循环展开(Loop Unrolling), 这样做的好处是可以减少内存循环的*迭代*次数，同时增加内层循环体内的指令数，这些计算和访存指令是无依赖的，对现代硬件流水线，一个循环体内尽量排多的无依赖指令，可以方便发挥乱序流水线(OoO)的指令多发射能力或者SIMD硬件并行能力，从而提高计算效率。

static void convdw3x3s1_pack8_int8_neon(const Mat& bottom_blob, Mat& top_blob, const Mat& kernel, const Option& opt)
{
    int w=bottom_blob.w;

    int outw=top_blob.w;
    int outh=top_blob.h;

    const int group=bottom_blob.c;

    #pragma omp parallel for num_threads(opt.num_threads)
    for (int g=0; g < group; g++)
{
        Mat out=top_blob.channel(g);

        const signed char* k0=kernel.row<const signed char>(g);

        int* outptr0=out.row<int>(0);
        int* outptr1=out.row<int>(1);

        const Mat img0=bottom_blob.channel(g);

        const signed char* r0=img0.row<const signed char>(0);
        const signed char* r1=img0.row<const signed char>(1);
        const signed char* r2=img0.row<const signed char>(2);
        const signed char* r3=img0.row<const signed char>(3);

        int8x8_t _k00=vld1_s8(k0);
        int8x8_t _k01=vld1_s8(k0 + 8);
        int8x8_t _k02=vld1_s8(k0 + 16);
        int8x8_t _k10=vld1_s8(k0 + 24);
        int8x8_t _k11=vld1_s8(k0 + 32);
        int8x8_t _k12=vld1_s8(k0 + 40);
        int8x8_t _k20=vld1_s8(k0 + 48);
        int8x8_t _k21=vld1_s8(k0 + 56);
        int8x8_t _k22=vld1_s8(k0 + 64);

        int i=0;
        for (; i + 1 < outh; i +=2)
{
            int j=0;
            for (; j + 1 < outw; j +=2)
{
                int8x16_t _r0001=vld1q_s8(r0);
                int8x16_t _r0203=vld1q_s8(r0 + 16);
                int8x16_t _r1011=vld1q_s8(r1);
                int8x16_t _r1213=vld1q_s8(r1 + 16);
                int8x16_t _r2021=vld1q_s8(r2);
                int8x16_t _r2223=vld1q_s8(r2 + 16);
                int8x16_t _r3031=vld1q_s8(r3);
                int8x16_t _r3233=vld1q_s8(r3 + 16);

                int16x8_t _s00=vmull_s8(vget_low_s8(_r0001), _k00);
                int16x8_t _s01=vmull_s8(vget_high_s8(_r0001), _k01);
                int16x8_t _s02=vmull_s8(vget_low_s8(_r0203), _k02);
                int16x8_t _s03=vmull_s8(vget_low_s8(_r1011), _k10);
                int16x8_t _s10=vmull_s8(vget_high_s8(_r0001), _k00);
                int16x8_t _s11=vmull_s8(vget_low_s8(_r0203), _k01);
                int16x8_t _s12=vmull_s8(vget_high_s8(_r0203), _k02);
                int16x8_t _s13=vmull_s8(vget_high_s8(_r1011), _k10);

                int16x8_t _s20=vmull_s8(vget_low_s8(_r1011), _k00);
                int16x8_t _s21=vmull_s8(vget_high_s8(_r1011), _k01);
                int16x8_t _s22=vmull_s8(vget_low_s8(_r1213), _k02);
                int16x8_t _s23=vmull_s8(vget_low_s8(_r2021), _k10);
                int16x8_t _s30=vmull_s8(vget_high_s8(_r1011), _k00);
                int16x8_t _s31=vmull_s8(vget_low_s8(_r1213), _k01);
                int16x8_t _s32=vmull_s8(vget_high_s8(_r1213), _k02);
                int16x8_t _s33=vmull_s8(vget_high_s8(_r2021), _k10);

                _s00=vmlal_s8(_s00, vget_high_s8(_r1011), _k11);
                _s01=vmlal_s8(_s01, vget_low_s8(_r1213), _k12);
                _s02=vmlal_s8(_s02, vget_low_s8(_r2021), _k20);
                _s03=vmlal_s8(_s03, vget_high_s8(_r2021), _k21);
                _s10=vmlal_s8(_s10, vget_low_s8(_r1213), _k11);
                _s11=vmlal_s8(_s11, vget_high_s8(_r1213), _k12);
                _s12=vmlal_s8(_s12, vget_high_s8(_r2021), _k20);
                _s13=vmlal_s8(_s13, vget_low_s8(_r2223), _k21);

                _s20=vmlal_s8(_s20, vget_high_s8(_r2021), _k11);
                _s21=vmlal_s8(_s21, vget_low_s8(_r2223), _k12);
                _s22=vmlal_s8(_s22, vget_low_s8(_r3031), _k20);
                _s23=vmlal_s8(_s23, vget_high_s8(_r3031), _k21);
                _s30=vmlal_s8(_s30, vget_low_s8(_r2223), _k11);
                _s31=vmlal_s8(_s31, vget_high_s8(_r2223), _k12);
                _s32=vmlal_s8(_s32, vget_high_s8(_r3031), _k20);
                _s33=vmlal_s8(_s33, vget_low_s8(_r3233), _k21);

                int16x8_t _s08=vmull_s8(vget_low_s8(_r2223), _k22);
                int16x8_t _s18=vmull_s8(vget_high_s8(_r2223), _k22);
                int16x8_t _s28=vmull_s8(vget_low_s8(_r3233), _k22);
                int16x8_t _s38=vmull_s8(vget_high_s8(_r3233), _k22);

                int32x4_t _sum00=vaddl_s16(vget_low_s16(_s00), vget_low_s16(_s01));
                int32x4_t _sum01=vaddl_s16(vget_high_s16(_s00), vget_high_s16(_s01));
                int32x4_t _sum02=vaddl_s16(vget_low_s16(_s02), vget_low_s16(_s03));
                int32x4_t _sum03=vaddl_s16(vget_high_s16(_s02), vget_high_s16(_s03));
                int32x4_t _sum10=vaddl_s16(vget_low_s16(_s10), vget_low_s16(_s11));
                int32x4_t _sum11=vaddl_s16(vget_high_s16(_s10), vget_high_s16(_s11));
                int32x4_t _sum12=vaddl_s16(vget_low_s16(_s12), vget_low_s16(_s13));
                int32x4_t _sum13=vaddl_s16(vget_high_s16(_s12), vget_high_s16(_s13));
                int32x4_t _sum20=vaddl_s16(vget_low_s16(_s20), vget_low_s16(_s21));
                int32x4_t _sum21=vaddl_s16(vget_high_s16(_s20), vget_high_s16(_s21));
                int32x4_t _sum22=vaddl_s16(vget_low_s16(_s22), vget_low_s16(_s23));
                int32x4_t _sum23=vaddl_s16(vget_high_s16(_s22), vget_high_s16(_s23));
                int32x4_t _sum30=vaddl_s16(vget_low_s16(_s30), vget_low_s16(_s31));
                int32x4_t _sum31=vaddl_s16(vget_high_s16(_s30), vget_high_s16(_s31));
                int32x4_t _sum32=vaddl_s16(vget_low_s16(_s32), vget_low_s16(_s33));
                int32x4_t _sum33=vaddl_s16(vget_high_s16(_s32), vget_high_s16(_s33));
                _sum00=vaddw_s16(_sum00, vget_low_s16(_s08));
                _sum01=vaddw_s16(_sum01, vget_high_s16(_s08));
                _sum10=vaddw_s16(_sum10, vget_low_s16(_s18));
                _sum11=vaddw_s16(_sum11, vget_high_s16(_s18));
                _sum20=vaddw_s16(_sum20, vget_low_s16(_s28));
                _sum21=vaddw_s16(_sum21, vget_high_s16(_s28));
                _sum30=vaddw_s16(_sum30, vget_low_s16(_s38));
                _sum31=vaddw_s16(_sum31, vget_high_s16(_s38));
                _sum00=vaddq_s32(_sum00, _sum02);
                _sum01=vaddq_s32(_sum01, _sum03);
                _sum10=vaddq_s32(_sum10, _sum12);
                _sum11=vaddq_s32(_sum11, _sum13);
                _sum20=vaddq_s32(_sum20, _sum22);
                _sum21=vaddq_s32(_sum21, _sum23);
                _sum30=vaddq_s32(_sum30, _sum32);
                _sum31=vaddq_s32(_sum31, _sum33);

                vst1q_s32(outptr0, _sum00);
                vst1q_s32(outptr0 + 4, _sum01);
                vst1q_s32(outptr0 + 8, _sum10);
                vst1q_s32(outptr0 + 12, _sum11);
                vst1q_s32(outptr1, _sum20);
                vst1q_s32(outptr1 + 4, _sum21);
                vst1q_s32(outptr1 + 8, _sum30);
                vst1q_s32(outptr1 + 12, _sum31);

                r0 +=16;
                r1 +=16;
                r2 +=16;
                r3 +=16;
                outptr0 +=16;
                outptr1 +=16;
            }
            for (; j < outw; j++)
{
                int8x8_t _r00=vld1_s8(r0);
                int8x8_t _r01=vld1_s8(r0 + 8);
                int8x8_t _r02=vld1_s8(r0 + 16);
                int8x8_t _r10=vld1_s8(r1);
                int8x8_t _r11=vld1_s8(r1 + 8);
                int8x8_t _r12=vld1_s8(r1 + 16);
                int8x8_t _r20=vld1_s8(r2);
                int8x8_t _r21=vld1_s8(r2 + 8);
                int8x8_t _r22=vld1_s8(r2 + 16);
                int8x8_t _r30=vld1_s8(r3);
                int8x8_t _r31=vld1_s8(r3 + 8);
                int8x8_t _r32=vld1_s8(r3 + 16);

                int16x8_t _s00=vmull_s8(_r00, _k00);
                int16x8_t _s01=vmull_s8(_r01, _k01);
                int16x8_t _s02=vmull_s8(_r02, _k02);
                int16x8_t _s03=vmull_s8(_r10, _k10);
                int16x8_t _s10=vmull_s8(_r10, _k00);
                int16x8_t _s11=vmull_s8(_r11, _k01);
                int16x8_t _s12=vmull_s8(_r12, _k02);
                int16x8_t _s13=vmull_s8(_r20, _k10);
                _s00=vmlal_s8(_s00, _r11, _k11);
                _s01=vmlal_s8(_s01, _r12, _k12);
                _s02=vmlal_s8(_s02, _r20, _k20);
                _s03=vmlal_s8(_s03, _r21, _k21);
                _s10=vmlal_s8(_s10, _r21, _k11);
                _s11=vmlal_s8(_s11, _r22, _k12);
                _s12=vmlal_s8(_s12, _r30, _k20);
                _s13=vmlal_s8(_s13, _r31, _k21);
                int16x8_t _s08=vmull_s8(_r22, _k22);
                int16x8_t _s18=vmull_s8(_r32, _k22);

                int32x4_t _sum00=vaddl_s16(vget_low_s16(_s00), vget_low_s16(_s01));
                int32x4_t _sum01=vaddl_s16(vget_high_s16(_s00), vget_high_s16(_s01));
                int32x4_t _sum02=vaddl_s16(vget_low_s16(_s02), vget_low_s16(_s03));
                int32x4_t _sum03=vaddl_s16(vget_high_s16(_s02), vget_high_s16(_s03));
                int32x4_t _sum10=vaddl_s16(vget_low_s16(_s10), vget_low_s16(_s11));
                int32x4_t _sum11=vaddl_s16(vget_high_s16(_s10), vget_high_s16(_s11));
                int32x4_t _sum12=vaddl_s16(vget_low_s16(_s12), vget_low_s16(_s13));
                int32x4_t _sum13=vaddl_s16(vget_high_s16(_s12), vget_high_s16(_s13));
                _sum00=vaddw_s16(_sum00, vget_low_s16(_s08));
                _sum01=vaddw_s16(_sum01, vget_high_s16(_s08));
                _sum10=vaddw_s16(_sum10, vget_low_s16(_s18));
                _sum11=vaddw_s16(_sum11, vget_high_s16(_s18));
                _sum00=vaddq_s32(_sum00, _sum02);
                _sum01=vaddq_s32(_sum01, _sum03);
                _sum10=vaddq_s32(_sum10, _sum12);
                _sum11=vaddq_s32(_sum11, _sum13);

                vst1q_s32(outptr0, _sum00);
                vst1q_s32(outptr0 + 4, _sum01);
                vst1q_s32(outptr1, _sum10);
                vst1q_s32(outptr1 + 4, _sum11);

                r0 +=8;
                r1 +=8;
                r2 +=8;
                r3 +=8;
                outptr0 +=8;
                outptr1 +=8;
            }

            r0 +=2 * 8 + w * 8;
            r1 +=2 * 8 + w * 8;
            r2 +=2 * 8 + w * 8;
            r3 +=2 * 8 + w * 8;

            outptr0 +=outw * 8;
            outptr1 +=outw * 8;
        }
        for (; i < outh; i++)
{
            int j=0;
            for (; j + 1 < outw; j +=2)
{
                int8x16_t _r0001=vld1q_s8(r0);
                int8x16_t _r0203=vld1q_s8(r0 + 16);
                int8x16_t _r1011=vld1q_s8(r1);
                int8x16_t _r1213=vld1q_s8(r1 + 16);
                int8x16_t _r2021=vld1q_s8(r2);
                int8x16_t _r2223=vld1q_s8(r2 + 16);

                int16x8_t _s00=vmull_s8(vget_low_s8(_r0001), _k00);
                int16x8_t _s01=vmull_s8(vget_high_s8(_r0001), _k01);
                int16x8_t _s02=vmull_s8(vget_low_s8(_r0203), _k02);
                int16x8_t _s03=vmull_s8(vget_low_s8(_r1011), _k10);
                int16x8_t _s10=vmull_s8(vget_high_s8(_r0001), _k00);
                int16x8_t _s11=vmull_s8(vget_low_s8(_r0203), _k01);
                int16x8_t _s12=vmull_s8(vget_high_s8(_r0203), _k02);
                int16x8_t _s13=vmull_s8(vget_high_s8(_r1011), _k10);
                _s00=vmlal_s8(_s00, vget_high_s8(_r1011), _k11);
                _s01=vmlal_s8(_s01, vget_low_s8(_r1213), _k12);
                _s02=vmlal_s8(_s02, vget_low_s8(_r2021), _k20);
                _s03=vmlal_s8(_s03, vget_high_s8(_r2021), _k21);
                _s10=vmlal_s8(_s10, vget_low_s8(_r1213), _k11);
                _s11=vmlal_s8(_s11, vget_high_s8(_r1213), _k12);
                _s12=vmlal_s8(_s12, vget_high_s8(_r2021), _k20);
                _s13=vmlal_s8(_s13, vget_low_s8(_r2223), _k21);
                int16x8_t _s08=vmull_s8(vget_low_s8(_r2223), _k22);
                int16x8_t _s18=vmull_s8(vget_high_s8(_r2223), _k22);

                int32x4_t _sum00=vaddl_s16(vget_low_s16(_s00), vget_low_s16(_s01));
                int32x4_t _sum01=vaddl_s16(vget_high_s16(_s00), vget_high_s16(_s01));
                int32x4_t _sum02=vaddl_s16(vget_low_s16(_s02), vget_low_s16(_s03));
                int32x4_t _sum03=vaddl_s16(vget_high_s16(_s02), vget_high_s16(_s03));
                int32x4_t _sum10=vaddl_s16(vget_low_s16(_s10), vget_low_s16(_s11));
                int32x4_t _sum11=vaddl_s16(vget_high_s16(_s10), vget_high_s16(_s11));
                int32x4_t _sum12=vaddl_s16(vget_low_s16(_s12), vget_low_s16(_s13));
                int32x4_t _sum13=vaddl_s16(vget_high_s16(_s12), vget_high_s16(_s13));
                _sum00=vaddw_s16(_sum00, vget_low_s16(_s08));
                _sum01=vaddw_s16(_sum01, vget_high_s16(_s08));
                _sum10=vaddw_s16(_sum10, vget_low_s16(_s18));
                _sum11=vaddw_s16(_sum11, vget_high_s16(_s18));
                _sum00=vaddq_s32(_sum00, _sum02);
                _sum01=vaddq_s32(_sum01, _sum03);
                _sum10=vaddq_s32(_sum10, _sum12);
                _sum11=vaddq_s32(_sum11, _sum13);

                vst1q_s32(outptr0, _sum00);
                vst1q_s32(outptr0 + 4, _sum01);
                vst1q_s32(outptr0 + 8, _sum10);
                vst1q_s32(outptr0 + 12, _sum11);

                r0 +=16;
                r1 +=16;
                r2 +=16;
                outptr0 +=16;
            }
            for (; j < outw; j++)
{
                int8x8_t _r00=vld1_s8(r0);
                int8x8_t _r01=vld1_s8(r0 + 8);
                int8x8_t _r02=vld1_s8(r0 + 16);
                int8x8_t _r10=vld1_s8(r1);
                int8x8_t _r11=vld1_s8(r1 + 8);
                int8x8_t _r12=vld1_s8(r1 + 16);
                int8x8_t _r20=vld1_s8(r2);
                int8x8_t _r21=vld1_s8(r2 + 8);
                int8x8_t _r22=vld1_s8(r2 + 16);

                int16x8_t _s0=vmull_s8(_r00, _k00);
                int16x8_t _s1=vmull_s8(_r01, _k01);
                int16x8_t _s2=vmull_s8(_r02, _k02);
                int16x8_t _s3=vmull_s8(_r10, _k10);
                _s0=vmlal_s8(_s0, _r11, _k11);
                _s1=vmlal_s8(_s1, _r12, _k12);
                _s2=vmlal_s8(_s2, _r20, _k20);
                _s3=vmlal_s8(_s3, _r21, _k21);
                int16x8_t _s4=vmull_s8(_r22, _k22);

                int32x4_t _sum0=vaddl_s16(vget_low_s16(_s0), vget_low_s16(_s1));
                int32x4_t _sum1=vaddl_s16(vget_high_s16(_s0), vget_high_s16(_s1));
                int32x4_t _sum2=vaddl_s16(vget_low_s16(_s2), vget_low_s16(_s3));
                int32x4_t _sum3=vaddl_s16(vget_high_s16(_s2), vget_high_s16(_s3));
                _sum0=vaddw_s16(_sum0, vget_low_s16(_s4));
                _sum1=vaddw_s16(_sum1, vget_high_s16(_s4));
                _sum0=vaddq_s32(_sum0, _sum2);
                _sum1=vaddq_s32(_sum1, _sum3);

                vst1q_s32(outptr0, _sum0);
                vst1q_s32(outptr0 + 4, _sum1);

                r0 +=8;
                r1 +=8;
                r2 +=8;
                outptr0 +=8;
            }

            r0 +=2 * 8;
            r1 +=2 * 8;
            r2 +=2 * 8;
        }
    }
}

NCNN使用的是显式GEMM实现，也就是有单独的im2col操作，用于构造输入矩阵。

核心详细代码注释如下：

    int w=bottom_blob.w;
    int inch=bottom_blob.c;

    int outw=top_blob.w;
    int outh=top_blob.h;
    const int size=outw * outh;

    const int maxk=kernel_w * kernel_h;

    // im2col
    // 创建一个新的输出张量，用于存储转换后的im2col格式的数据, 维度为(size, maxk, inch)三维dim
    Mat bottom_im2col(size, maxk, inch, 4u, 1, opt.workspace_allocator);

{
        // 计算每行最后一个元素与下一行第一个元素之间的距离，用于跳过padding部分的数据
        const int gap=w * stride_h - outw * stride_w;

        #pragma omp parallel for num_threads(opt.num_threads)
        for (int p=0; p < inch; p++)
{
            const Mat img=bottom_blob.channel(p);
            float* ptr=bottom_im2col.channel(p); //取bottom_im2col的一个channel

            for (int u=0; u < kernel_h; u++) //遍历卷积核index
{
                for (int v=0; v < kernel_w; v++)
{
                    // 选中第一个卷积滑窗位置对应的featuremap的（u, v）位置，作为下面循环的起始点
                    const float* sptr=img.row<const float>(dilation_h * u) + dilation_w * v;

                    for (int i=0; i < outh; i++) //在bottom_im2col.channel[p]的 height方向移动
{
                        int j=0;
                        for (; j < outw; j++)
{
                            ptr[0]=sptr[0];     //选中卷积滑窗中对应的feature map的第一个元素

                            sptr +=stride_w;     //相当于卷积滑窗移动
                            ptr +=1;             //height方向移动
                        }

                        sptr +=gap;              //跳过padding部分，位移到feature map的下一行
                    }
                }
            }
        }
    }

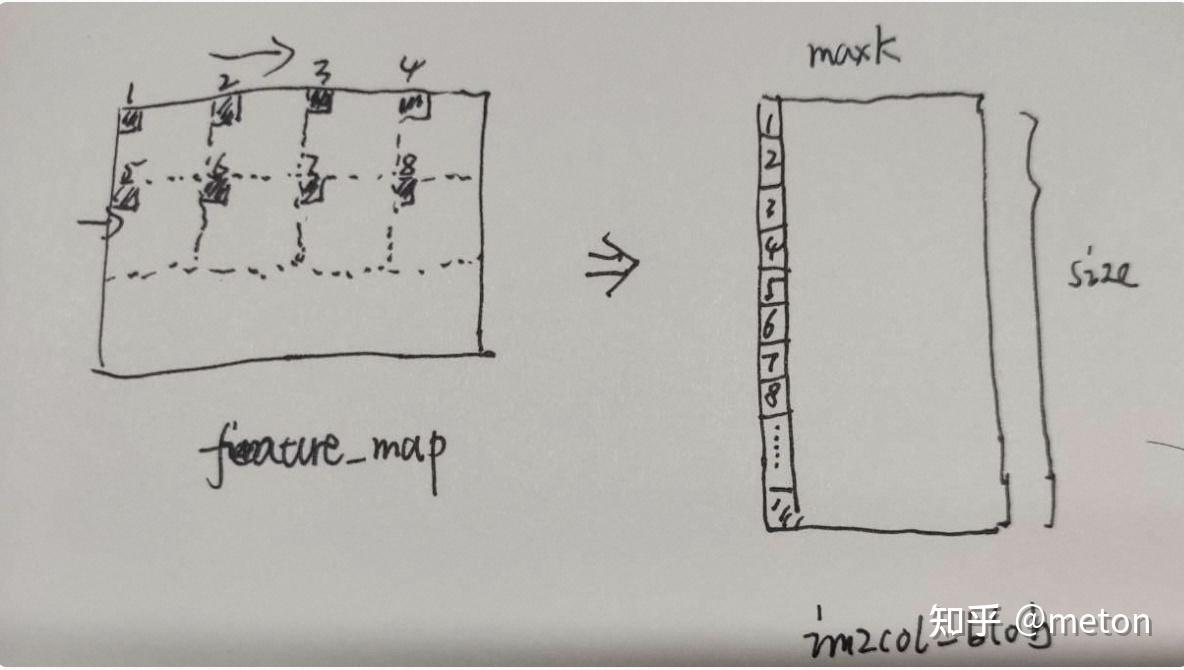
可以看到ncnn每次先填充im2col_blob的一列。

这里截取的是 ncnn中 mips后端的convolution_sgemm.h代码的通用实现部分，没有使用msa加速，代码整体注释如下:

static void im2col_sgemm_msa(const Mat& bottom_im2col, Mat& top_blob, const Mat& kernel, const Mat& _bias, const Option& opt)
{
    // Mat bottom_im2col(size, maxk, inch, 4u, 1, opt.workspace_allocator);

    const int size=bottom_im2col.w;
    const int maxk=bottom_im2col.h;
    const int inch=bottom_im2col.c;

    const int outch=top_blob.c; 

    const float* bias=_bias;

    // permute (size, maxk, inch ) -> (maxk, inch, size ) **注意**这个的维度是按ncnn mat格式表示 (width, height, channel)
    // 使得 (maxk, inch) 平面数据排布连续, (maxk, inch) 平面的一行数，卷积核某个通道，Kw*Kh区域的所有元素
    Mat tmp;
    if (size >=4)
        tmp.create(4 * maxk, inch, size / 4 + size % 4, 4u, 1, opt.workspace_allocator);
    else
        tmp.create(maxk, inch, size, 4u, 1, opt.workspace_allocator);
{
        int nn_size=size / 4;

        #pragma omp parallel for num_threads(opt.num_threads)
        for (int ii=0; ii < nn_size; ii++)
{
            int i=ii * 4;

            float* tmpptr=tmp.channel(i / 4);

            for (int q=0; q < inch; q++)
{
                const float* img0=(const float*)bottom_im2col.channel(q) + i;

                for (int k=0; k < maxk; k++)
{

                    tmpptr[0]=img0[0];
                    tmpptr[1]=img0[1];
                    tmpptr[2]=img0[2];
                    tmpptr[3]=img0[3];
                    img0 +=size;
                    tmpptr +=4;
                }
            }
        }

        int remain_size_start=nn_size * 4;

        #pragma omp parallel for num_threads(opt.num_threads)
        for (int i=remain_size_start; i < size; i++)
{
            float* tmpptr=tmp.channel(i / 4 + i % 4);

            for (int q=0; q < inch; q++)
{
                const float* img0=(const float*)bottom_im2col.channel(q) + i;

                for (int k=0; k < maxk; k++)
{
                    tmpptr[0]=img0[0];
                    img0 +=size;
                    tmpptr +=1;
                }
            }
        }
    }

    int nn_outch=outch >> 1;  // /2
    int remain_outch_start=nn_outch << 1; // *2

    #pragma omp parallel for num_threads(opt.num_threads)
    for (int pp=0; pp < nn_outch; pp++)  //外层循环，每次处理output tensor的两个通道的输出
{
        int p=pp * 2;

        float* outptr0=top_blob.channel(p);
        float* outptr1=top_blob.channel(p + 1);

        const float zeros[2]={0.f, 0.f};
        const float* biasptr=bias ? bias + p : zeros;

        int i=0;
        for (; i + 3 < size; i +=4)       //内层循环 每次处理tmp的size维度(data patch维度)的四个元素, 结合外循环，也就是每次输出八个结果. 
{
            //tmp 维度(maxk, inch, size ) **注意**这个的维度是按ncnn mat格式表示 (width, height, channel)
            //tmpptr相当于选中 tmp(maxk, inch, i:i+4 )的一个块
            const float* tmpptr=tmp.channel(i / 4);  

            //kptr相当于选中 kernel（inch*maxk, p: p+2）的一个块, 相当于两个滤波器的数据
            const float* kptr=kernel.channel(p / 2); //kernel维度 ( inch*maxk, outch)

            int nn=inch * maxk;         //inch always > 0

            float sum00=biasptr[0];     //sum 先赋值bias
            float sum01=biasptr[0];
            float sum02=biasptr[0];
            float sum03=biasptr[0];

            float sum10=biasptr[1];
            float sum11=biasptr[1];
            float sum12=biasptr[1];
            float sum13=biasptr[1];

            for (int q=0; q < nn; q++)  //nn=maxk * inch  遍历 tmp的(maxk, inch)平面的每一个位置
{
                /*
                它会提前将 tmpptr +16 处的数据预取到 CPU 的缓存中，以便之后访问时能够更快地获取数据。这是一种数据预取（data prefetching）技术，
                可以提高程序的性能，特别是对于数据访问频繁的程序。在这个代码中，它的作用是加快下一次数据访问速度，提高循环遍历 tmp 和 kernel 的效率。
                */
                __builtin_prefetch(tmpptr + 16); 
                __builtin_prefetch(kptr + 8);
                float k0=kptr[0];
                float k1=kptr[1];

                //卷积的一个点，去同时卷四个 data patch的对应位置的点
                //最内层循环, 一个K0被重用四次
                sum00 +=tmpptr[0]* k0;  //乘累加, sum +=data * k 
                sum01 +=tmpptr[1]* k0;
                sum02 +=tmpptr[2]* k0;
                sum03 +=tmpptr[3]* k0;

                sum10 +=tmpptr[0]* k1;
                sum11 +=tmpptr[1]* k1;
                sum12 +=tmpptr[2]* k1;
                sum13 +=tmpptr[3]* k1;
                tmpptr +=4;
                kptr +=2;
            }

            outptr0[0]=sum00;
            outptr0[1]=sum01;
            outptr0[2]=sum02;
            outptr0[3]=sum03;

            outptr1[0]=sum10;
            outptr1[1]=sum11;
            outptr1[2]=sum12;
            outptr1[3]=sum13;

            outptr0 +=4;
            outptr1 +=4;
        }

        // 处理不足4倍数的剩余部分
        for (; i < size; i++)
{
            const float* tmpptr=tmp.channel(i / 4 + i % 4);
            const float* kptr=kernel.channel(p / 2);

            int nn=inch * maxk; // inch always > 0

            float sum0=biasptr[0];
            float sum1=biasptr[1];

            for (int q=0; q < nn; q++)
{
                __builtin_prefetch(tmpptr + 4);
                __builtin_prefetch(kptr + 8);
                sum0 +=tmpptr[0]* kptr[0];
                sum1 +=tmpptr[0]* kptr[1];
                tmpptr++;
                kptr +=2;
            }

            outptr0[0]=sum0;
            outptr1[0]=sum1;

            outptr0++;
            outptr1++;
        }
    }


    #pragma omp parallel for num_threads(opt.num_threads)
    for (int p=remain_outch_start; p < outch; p++)
{
        float* outptr0=top_blob.channel(p);

        const float bias0=bias ? bias[p]: 0.f;

        int i=0;
        for (; i + 3 < size; i +=4)
{
            const float* tmpptr=tmp.channel(i / 4);

            const float* kptr=kernel.channel(p / 2 + p % 2);

            int nn=inch * maxk; // inch always > 0

            float sum0=bias0;
            float sum1=bias0;
            float sum2=bias0;
            float sum3=bias0;

            for (int q=0; q < nn; q++)
{
                __builtin_prefetch(tmpptr + 16);
                __builtin_prefetch(kptr + 4);
                sum0 +=tmpptr[0]* kptr[0];
                sum1 +=tmpptr[1]* kptr[0];
                sum2 +=tmpptr[2]* kptr[0];
                sum3 +=tmpptr[3]* kptr[0];
                tmpptr +=4;
                kptr++;
            }

            outptr0[0]=sum0;
            outptr0[1]=sum1;
            outptr0[2]=sum2;
            outptr0[3]=sum3;

            outptr0 +=4;
        }

        for (; i < size; i++)
{
            const float* tmpptr=tmp.channel(i / 4 + i % 4);

            const float* kptr=kernel.channel(p / 2 + p % 2);
            int nn=inch * maxk; // inch always > 0

            float sum0=bias0;

            for (int q=0; q < nn; q++)
{
                sum0 +=tmpptr[0]* kptr[0];
                tmpptr++;
                kptr++;
            }

            outptr0[0]=sum0;

            outptr0++;
        }
    }
}

总结：

GEMM代码使用的是多输出实现，每次外层循环处理两个通道的输出，内层循环每次处理四个通道的数据，因此每次计算得到8个数值结果。
这种多输出方式会使代码难读懂，但是可以提高性能。原因是：

可以减少内存循环的*迭代*次数，同时增加内层循环体内的指令数（相当于一种Loop Unrolling技巧），这些指令是无依赖的，对现代硬件流水线，一个循环体内尽量排多的无依赖指令，可以方便发挥乱序流水线(OoO)的指令多发射能力，从而提高计算效率。
如果硬件有SIMD能力(如MIPS的MSA)，循环体内类似的多条计算操作(相同操作，但是操作的是不同数据，也就是无依赖)，其实可以用一条SIMD向量指令来替代，从而进一步提高计算效率。实现方式也更符合现代CPU的SIMD指令集特性，可以充分利用向量化指令加速计算。
前面小节的GEMM计算示例图讲解，都是从算法原理和概念去理解，但是落到具体硬件，往往为了考虑高效，实现细节和原理概念大相径庭，第一层是理解算法原理，第二层是理解算法原理+理解硬件能力，写出高效的代码，尽管代码难懂。

另外核心计算代码前，总会有一些矩阵的数据重排操作，例如代码中将bottom_im2col从(size，maxk, inch) reshape成(maxk, inch, size) 维度(这里的维度排序是按NCNN的mat结构格式( width, height channel))，使得 (maxk, inch) 平面数据排布连续，增加取数cache友好性。数据重排本身有一定时间开销，因此获得加速的前提是计算部分足够密集，才能分摊数据重排的开销。
代码循环中，计算前，调用 __builtin_prefetch()，它会提前将*指定的数据*附近的一段数据(按Cache line 一行的数据量) 全部先预取到 CPU Cache缓存中，以便之后访问时能够更快地获取数据。这是一种微架构设计中的一种数据预取（data prefetching）技术，可以提高程序的性能，特别是对于数据访问频繁的程序。在这个代码中，它的作用是加快下一次数据访问速度。

按照前面小节对wingrad计算的理解，去看ncnn代码，会发现一脸懵逼，因此具体实现和直观理解推导并不一样。

NCNN是直接将Wingrad的计算矩阵化，下面先进行代码理解。

对于原先的初级形式：

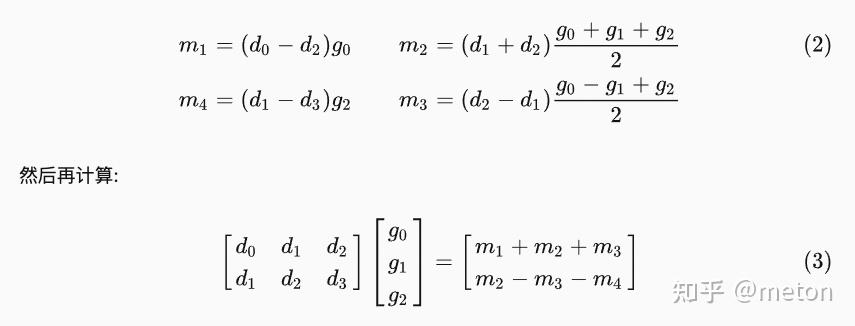
对于二维wingrad, 可以写成矩阵形式,如下图:

NCNN在计算输出Y的时候，是将输入d和卷积参数g与几个系数矩阵进行了矩阵乘 + 矩阵元素点乘的操作。

最后其实就是U V矩阵的获得，然后进行矩阵乘 + 矩阵元素点乘的操作。

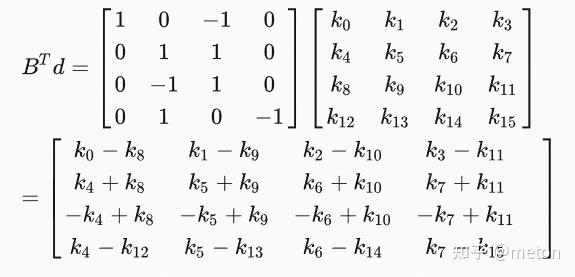
而在在计算 BTd 的时候, 由于 BT 里有很多0和正负1, 其实我是可以不用乘的. 固定死写成加法即可, 这样原本所需要的64次乘法我全部都可以省掉了, 加法也从48次变成32次。Gg矩阵的计算也可以在离线进行计算，固化成常量系数矩阵。

简化版本的wingrad算法实现，可以写成如下：

float G[12]={1, 0, 0,
0.5, 0.5, 0.5,
0.5, -0.5, 0.5,
0, 0, 1};
float GT[12]={1, 0.5, 0.5, 0,
0, 0.5, -0.5, 0,
0, 0.5, 0.5, 1};
//矩阵乘
void dot(float* A, int row_A, int col_A, float* B, int row_B, int col_B, float* C){
    assert(col_A==row_B);              // && row_A==col_B
    //由矩阵相乘，要求f2=s1，以下用f2
    for (int i=0; i < row_A; i++)      // i表示第i行
        for (int j=0; j < col_B; j++)  // j表示第j列
            //  C[i*col_A + j]=0;        //在这里 result[i][j]=result[i*f2+j];
            for (int p=0; p < col_A; p++)
                C[i * col_B + j]+=A[i * col_A + p]* B[p * col_B + j];
}
//对应点相乘
void multi(float* A, int row_A, int col_A, float* B, int row_B, int col_B, float* C){
    assert(row_A==row_B && col_A==col_B);
    for (int i=0; i < row_A; i++)
        for (int j=0; j < col_A; j++)
            C[col_A * i + j]=A[col_A * i + j]* B[col_A * i + j];
}
?
void winograd6_transforme_g(float* g, float* transformed_g){
float Gg[12]={0};
?
dot(G, 4, 3, g, 3, 3, Gg);  //先计算得到U=GgGT
dot(Gg, 4, 3, GT, 3, 4, transformed_g);
}
?
void winograd6(float* U, float* d, float* result){
float BTd[16]={0};
float V[16]={0};
float UV[16]={0};
float ATUV[8]={0};
?
// start dot(BT, 4, 4, d, 4, 4, BTd);
BTd[0]=d[0]- d[8];
BTd[1]=d[1]- d[9];
BTd[2]=d[2]- d[10];
BTd[3]=d[3]- d[11];
?
BTd[4]=d[4]+ d[8];
BTd[5]=d[5]+ d[9];
BTd[6]=d[6]+ d[10];
BTd[7]=d[7]+ d[11];
?
BTd[8]=-d[4]+ d[8];
BTd[9]=-d[5]+ d[9];
BTd[10]=-d[6]+ d[10];
BTd[11]=-d[7]+ d[11];
?
BTd[12]=d[4]- d[12];
BTd[13]=d[5]- d[13];
BTd[14]=d[6]- d[14];
BTd[15]=d[7]- d[15];
// end dot(BT, 4, 4, d, 4, 4, BTd);
?
// start dot(BTd, 4, 4, B, 4, 4, V);
V[0]=BTd[0]- BTd[2];
V[4]=BTd[4]- BTd[6];
V[8]=BTd[8]- BTd[10];
V[12]=BTd[12]- BTd[14];
?
V[1]=BTd[1]+ BTd[2];
V[5]=BTd[5]+ BTd[6];
V[9]=BTd[9]+ BTd[10];
V[13]=BTd[13]+ BTd[14];
?
V[2]=-BTd[1]+ BTd[2];
V[6]=-BTd[5]+ BTd[6];
V[10]=-BTd[9]+ BTd[10];
V[14]=-BTd[13]+ BTd[14];
?
V[3]=BTd[1]- BTd[3];
V[7]=BTd[5]- BTd[7];
V[11]=BTd[9]- BTd[11];
V[15]=BTd[13]- BTd[15];
// end dot(BTd, 4, 4, B, 4, 4, V);
?
multi(U, 4, 4, V, 4, 4, UV);
?
// start dot(AT, 2, 4, UV, 4, 4, ATUV);
ATUV[0]=UV[0]+ UV[4]+ UV[8];
ATUV[1]=UV[1]+ UV[5]+ UV[9];
ATUV[2]=UV[2]+ UV[6]+ UV[10];
ATUV[3]=UV[3]+ UV[7]+ UV[11];

ATUV[4]=UV[4]- UV[8]- UV[12];
ATUV[5]=UV[5]- UV[9]- UV[13];
ATUV[6]=UV[6]- UV[10]- UV[14];
ATUV[7]=UV[7]- UV[11]- UV[15];
// end dot(AT, 2, 4, UV, 4, 4, ATUV);
?
// start dot(ATUV, 2, 4, A, 4, 2, result);
result[0]+=(ATUV[0]+ ATUV[1]+ ATUV[2]);
result[2]+=(ATUV[4]+ ATUV[5]+ ATUV[6]);
result[1]+=(ATUV[1]- ATUV[2]- ATUV[3]);
result[3]+=(ATUV[5]- ATUV[6]- ATUV[7]);
// end dot(ATUV, 2, 4, A, 4, 2, result);
}
?
int main(int argc, char const* argv[]){
float g[]={1, 2, 3, 
4, 5, 6, 
7, 8, 9};
float d[]={1, 2, 3, 4, 
5, 6, 7, 8, 
9, 10, 11, 12, 
13, 14, 15, 16};
float result[4]={0};
?
float* transformed_g=calloc(16, sizeof(float));
winograd6_transforme_g(g, transformed_g);
?
winograd6(transformed_g, d, result);
return 0;
}

可以看出，在工程实现上，wingrad算法中被转变为矩阵运算，总结来说主要有以下几个步骤

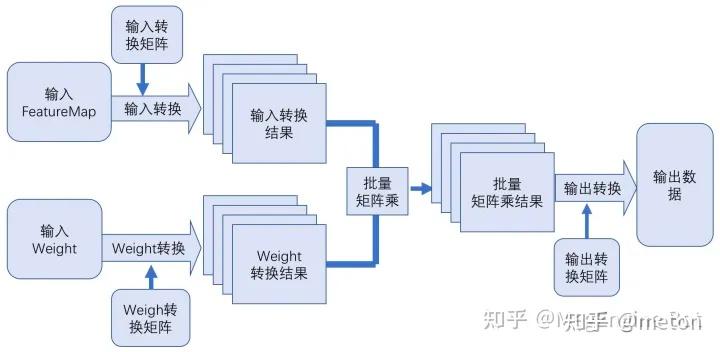
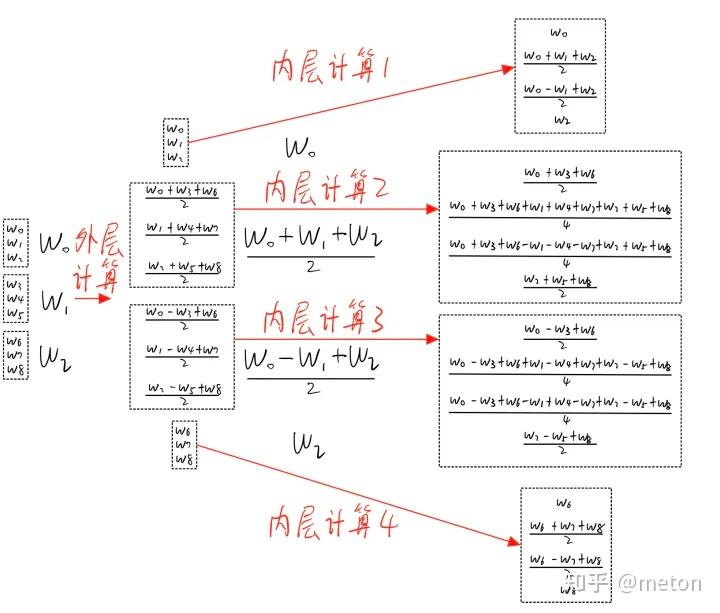
以wingrad3x3_23卷积为例，用几张图详细说明整个过程，会更加清楚: 注意wingrad3x3_23，是指卷积核3x3, 输入的一个tile大小为4x4, 输出tile大小为2x2 。

weight和input转化过程

上半部分是 weights 的转换，下半部分是输入 FeatureMap 的转换。其中包括了 Winograd 转换以及 relayout 的过程。对于 weights 的转换，首先通过 Winograd 变换矩阵 G 和 GT 分别将 3x3 的 weight 转换为 4x4 的矩阵，然后将该矩阵中相同位置的点（如图中蓝色为位置 1 的点）relayout 为一个 IC*OC 的矩阵，最终形成 4x4=16 个转换之后 weights 矩阵。

对于 FeatureMap 的转换，首先将输入 FeatureMap 按照 4x4 tile 进行切分，然后将每个 tile 通过 B 和 BT 转换为 4x4 的矩阵，矩阵 B 和 BT 为 FeatureMap 对应的 Winograd 变换矩阵，然后进行与 weight 处理相似的 relayout，转换为 16 个 nr_tiles*IC 的 FeatureMap 矩阵。

矩阵运算操作

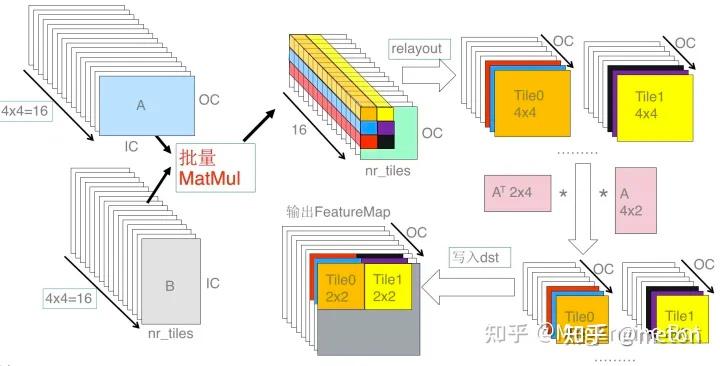
如上图所示，将上述转换后两批矩阵做矩阵乘，得到 16 个 nr_tiles*OC 的矩阵，然后将相同位置的 16 个点转换为 nr_tiles*OC 个 4x4 矩阵，再使用输出的 Winograd 变换矩阵 A 和 AT 将这些 4x4 的矩阵转换为 2x2 的输出矩阵，最后将这些矩阵写回输出矩阵中就可以得到 Winograd 卷积的最终结果。

更多资料:

NCNN中conv3x3s1_winograd64_transform_kernel_neon5 和conv3x3s1_winograd64_neon5的代码实现讲解可以参考博客：

https://zhuanlan.zhihu.com/p/524355496

https://zhuanlan.zhihu.com/p/381839221

https://zhuanlan.zhihu.com/p/29119239

https://www.zhihu.com/question/54149221/answer/192025860

https://zhuanlan.zhihu.com/p/532187602

https://zhuanlan.zhihu.com/p/38575159

有许多参考链接内嵌在正文中，在这里未列出来。

全链路DL加速的一些问题和领域总述：

https://zhuanlan.zhihu.com/p/101544149

上一条：抖音营销，餐饮火锅店营销方案？下一条：抖音极速版官方下载_2