目前了解到两个可能的原因:1)Adam系列更快。2)NLP模型是稀疏的,在稀疏模型上使用AdamW效果比较好(但还没有找到相关的论文)。
请问上面两点原因正确吗?如果第二点正确,有没有文献出处呢?是否还有其它原因?
题主提到的两点原因都是正确的:
自适应学习率: Adam 优化器利用梯度的第一矩和第二矩估计值,单独调整每个权重的学习率。这种自适应学习率方法能带来更高效的更新和更快的收敛。
高效梯度下降: 与需要对所有参数进行相同大小更新的 SGD 不同,Adam 通过对频繁更新的参数进行较小的更新和对不频繁更新的参数进行较大的更新来实现高效梯度下降。
对初始学习率的依赖性更小: Adam 优化器对初始学习率的敏感度较低,从而减少了用于超参数调整的时间。
修正权重衰减: Adam 和 AdamW 的主要区别在于它们如何处理权重衰减(正则化的一种形式)。在 Adam 中,权重衰减是在计算梯度之前应用的,这会导致次优结果。AdamW 在计算梯度后才应用权重衰减,这是一种更正确的实现方式。
改进了泛化: 通过正确应用权重衰减,AdamW 的泛化效果往往比 Adam 更好,尤其是在较大的模型或数据集上。
更好的收敛性: 经验结果表明,AdamW 比 Adam 收敛得更快,而且能得到更好的解决方案,尤其是在像 NLP 这样梯度稀疏的任务上。
Weight Prediction Boosts the convergence of AdamW (2023)
Understanding Adamw through Proximal Methods and Scale-Freeness (2022)
Decoupled weight decay regularization (2017)
谢邀!最近雄哥公司来了不少新人,在培训大家使用优化器,一般根据不同的目标、不同的模型,去灵活选择,虽然AdamW很优秀,但有些情况下SGD会更胜任,特别是在计算资源有限的情况下。
一般雄哥会从这些角度分析,主要有这几个区别:
1、自适应学习率: AdamW通过自适应地调整每个参数的学习率,可以更好地适应不同参数的变化范围。相比之下,SGD需要手动设置学习率,并且在训练过程中可能需要进行调整。
2、动量和二次矩估计: AdamW结合了动量(momentum)和二次矩估计(second moment estimation),使得在参数空间中能够更快地收敛到局部最优点。这对于复杂的NLP模型来说尤其重要,因为NLP任务通常涉及高维的参数空间。
3、稀疏梯度处理: 在NLP任务中,输入数据通常是稀疏的,而AdamW能够处理稀疏梯度的情况,这使得它在NLP任务中更具优势。
4、权重衰减: AdamW引入了权重衰减机制,有助于防止模型的权重过度增长,从而减轻过拟合的风险。这对于大型的NLP模型尤其重要,因为这些模型容易过拟合。
5、偏置修正: AdamW对梯度的一阶矩和二阶矩进行了偏置修正,减少了初始训练阶段的偏差,提高了训练的稳定性。
雄哥专注NLP领域多年啦!行业初期,希望更多人加入,推进行业发展!
一意公众号四大功能!
#1 高质量数据集
我搭建了一个训练数据共享平台,目前已收录法律、金融、医疗、教育、诗词等超1T的人工标注数据集,还可以通过群内共享。
#2 报错或问题解决
你可能像我们NLP学习群中的同学一样,遇到各种报错或问题,我每天挑选5条比较有代表性的问题及解决方法贴出来,供大家避坑;每天更新,欢迎来蹲!
#3 运算加速
还有同学是几年前的老爷机/笔记本,显卡不好,我们应用了动态运输技术框架,直接提升超40%运算效率,无显卡2g内存就能跑,直接焕发第二春;
#4 微调训练教程
如果你还不知道该怎么微调训练模型,在这里还可以学训练和微调,跟着一步步做,你也能把大模型的知识真正应用到实处,产生价值。
题主思考的两个角度是对的,下面是鄙人查阅资料以及整合GPT的回答所得。
从优化器的角度考虑,有以下几个原因:
①自适应学习率:AdamW 结合了 Adam 优化器和权重衰减(Weight Decay)的概念。Adam 优化器具有自适应学习率的特性,可以根据参数的不同情况自动调整每个参数的学习率。相比之下,SGD 需要手动调整学习率,且对于不同的参数可能需要不同的学习率。
②动量优化:AdamW 还使用了动量优化的方法,可以加速模型的收敛过程。动量优化有助于处理非凸优化问题,并帮助模型跳出局部最小值,更好地搜索全局最优解。
③权重衰减:AdamW 在 Adam 的基础上增加了权重衰减(L2 正则化)的项,用于控制模型的复杂度并防止过拟合。这对于 NLP 模型来说尤为重要,因为它们通常具有大量的参数和复杂的结构,容易产生过拟合现象。
④平稳性:相对于 SGD,AdamW 通常具有更平稳的训练过程。AdamW 通过计算梯度的一阶和二阶矩估计来调整学习率,可以更精确地更新参数,从而更稳定地优化模型。
从自然语言处理(NLP)的角度考虑有以下几个原因:
①适应文本数据特点:NLP任务中的文本数据通常具有大量的稀疏特征和高维度。AdamW 可以根据参数的梯度情况自适应地调整学习率,对于稀疏特征更加敏感,从而提高训练的效率和收敛速度。
②处理复杂模型结构:在 NLP 中,常见的模型,如循环神经网络(RNN)、长短期记忆网络(LSTM)和变压器(Transformer),具有复杂的结构和大量的参数。AdamW 的动量更新策略能够帮助模型更好地处理这种复杂性,加速收敛过程并减少震荡。
③控制模型复杂度:NLP 模型往往面临过拟合问题,即模型在训练数据上表现良好,但在测试数据上表现较差。AdamW 的权重衰减机制有助于控制模型的复杂度,通过给予较大的权重衰减项(L2 正则化),在优化过程中防止模型过度拟合。
④平稳性和稳定性:AdamW 结合了 Adam 优化器的特点,通过计算梯度的一阶和二阶矩估计来自适应地调整学习率。这种特性使得优化过程更加平稳,减少了极值点附近的震荡,有助于模型更好地捕捉数据中的模式和结构。
以上。
weight decay在优化器中的使用如下:
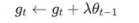
其实就是加入了l2正则,l2正则在求导后是2θ,当对其进行加权后变为λθ
每次梯度更新都会带有前几次梯度方向的惯性,使梯度的变化更加平滑,这一点上类似一阶马尔科夫假设(当前状态只和上一个状态有关)
通过计算梯度的指数加权平均数(加权移动平均)来积累之前的动量,进而替代真正的梯度,减少震荡问题
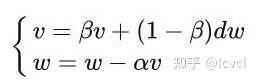
动量参数v本质上就是到目前为止所有历史梯度值的加权平均,距离越远,权重越小
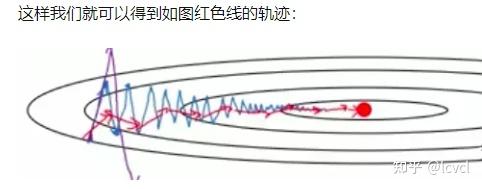
蓝色线为sgd的图
β 越小,噪音越多,但是更容易出现奇异值。
β 越大,得到的曲线越平坦
一般β取0.9
NGA算法类似用已得到的前两个梯度对当前梯度进行修正(类似二阶马尔科夫假设)
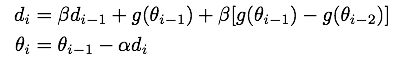
NAG算法会根据此次梯度(i-1)和上一次梯度(i-2)的差值对Momentum算法得到的梯度进行修正
两次梯度的差值为正,证明梯度再增加,我们有理由相信下一个梯度会继续变大;
相反两次梯度的差值为负,我们有理由相信下一个梯度会继续变小
使用变量st来累加过去的梯度方差
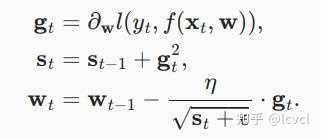
η是学习率,?是一个为维持数值稳定性而添加的常数,用来确保不会除以0。初始化s0=0
学习率对梯度影响大,学习率最终会变得很小,因为分母会不断积累
解决Adagrad分母会不断积累,这样学习率就会收缩并最终会变得非常小的问题。
历史的梯度信息使用decaying average的方式进行累计
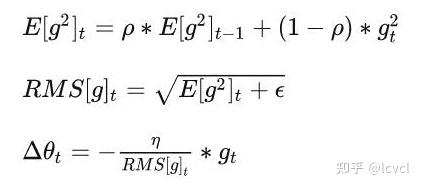
RMSprop 通常与动量一起使用,可以理解为 Rprop 对小批量设置的适应,见torch中的实现

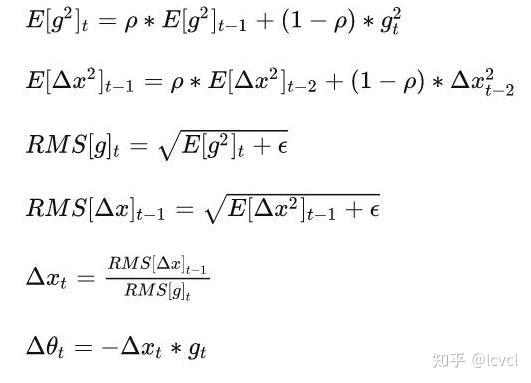
Adadelta使用两个状态变量,
st用于存储梯度导数平方的泄露平均值,
Δxt用于存储模型本身中参数变化导数平方的泄露平均值

●训练初中期,加速效果不错,很快
●训练后期,反复在局部最小值附近抖动
梯度和梯度的平方
Adma吸收了Adagrad(自适应学习率的梯度下降算法)和动量梯度下降算法的优点,既能适应稀疏梯度(即自然语言和计算机视觉问题),又能缓解梯度震荡的问题
SGD with momentum在SGD的基础上增加了一阶动量,AdaGrad和AdaDelta在SGD的基础上增加了二阶动量,把一阶动量和二阶动量都用起来,就是Adam了Adaptive+Momentum
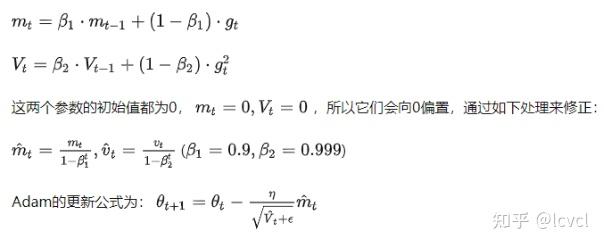

梯度衰减与学习率解耦,在weight decay的地方乘学习率
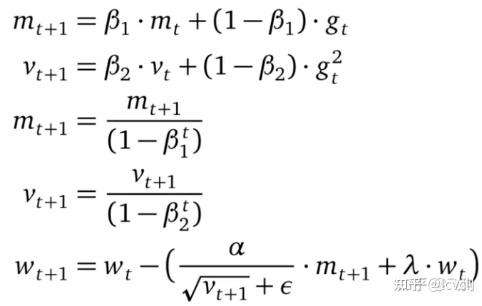
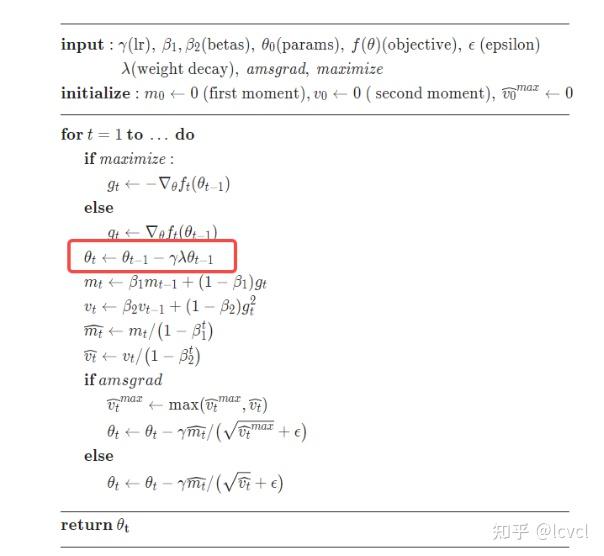
区别是在weight decay的时候adamw引入了学习率
adam将weight引入到了累积梯度里面
adamw没有
Adamw 即 Adam + weight decate ,效果与 Adam + L2 正则化相同,但是计算效率更高,之前的 L2 正则化需要在 loss 中加入正则项再算梯度,反向传播,AdamW 直接将正则项的梯度加入反向传播的公式中,减少在 loss 中加正则项这一步
v/(1-β)t 的原因,是因为初始时v会很小,为了对其进行放大才会使用
如果在训练过程中一直保持学利率不发生变化,其会以非常慢的速度根据梯度的值进行变化
一般情况下loss变小梯度就会变小,梯度由损失函数的偏导进行计算
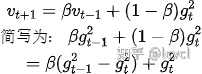
此时vt+1中近似包括梯度的变化率,即w的二阶导
公司名称: 天富娱乐-天富医疗器械销售公司
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号