关于多目标优化，有何经典的入门书籍和论文，求推荐？

关于多目标优化，有何经典的入门书籍和论文，求推荐，数学底子很差，需要用到这个方法做课题，真是头疼，希望大神解答。 @Fan You @撩妹狂魔 @龚觉 @Robin Shen @善善

多目标的经典算法应该是基因算法吧，计算Parento Front用population based的方法， 经典论文比如K. Deb的NSGA-II.

没有可推荐的中英文书。但是多目标优化问题可以参考勤务表优化问题，里面的目标函数设定思想和启发式算法是一样的

推荐最新关于《多任务学习》综述，非常适合入门者进行学习和了解多目标优化。

最新《多任务学习》综述，39页pdf - 专知VIP

许多现实世界中的优化问题本质上都是多目标的。 多目标进化算法是解决多目标优化问题的一种广泛使用的算法框架，而多任务学习可以自然地建模为多目标优化问题。

随着任务复杂程度和数据规模的增加,对人工标注数据的数量和质量也提出了更高的要求,造成了标注成本和难度的增大。同时,单一任务的独立学习往往忽略了来自其他任务的经验信息,致使训练冗余重复因而导致了学习资源的浪费,也限制了其性能的提升。

为了缓解这些问题,属于迁移学习范畴的多任务学习方法逐渐引起了研究者的重视。与单任务学习只使用单个任务的样本信息不同,多任务学习假设不同任务数据分布之间存在一定的相似性,在此基础上通过共同训练和优化建立任务之间的联系。

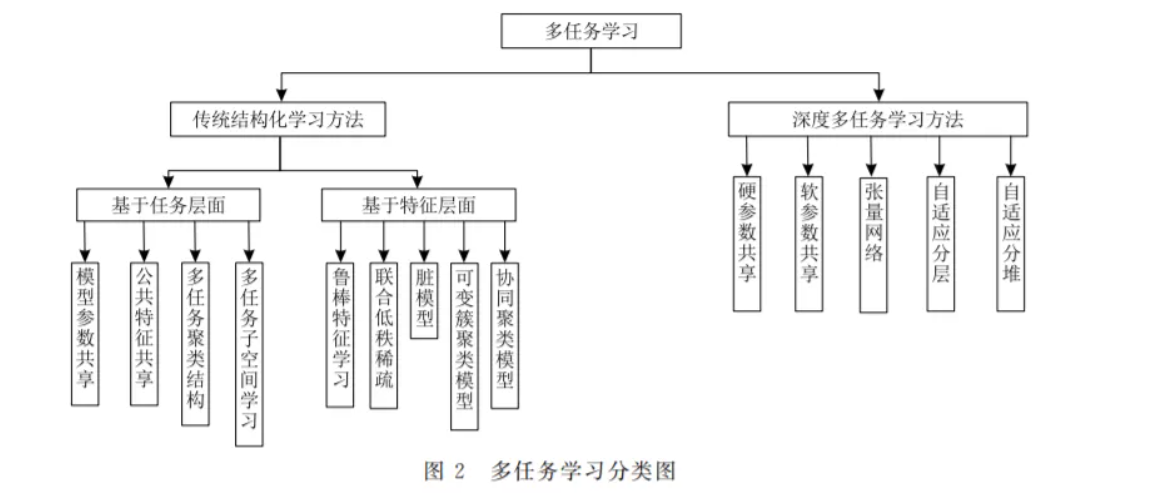
这种训练模式充分促进任务之间的信息交换并达到了相互学习的目的,尤其是在各自任务样本容量有限的条件下,各个任务可以从其它任务获得一定的启发,借助于学习过程中的信息迁移能间接利用其它任务的数据,从而缓解了对大量标注数据的依赖,也达到了提升各自任务学习性能的目的。在此背景之下,本文首先介绍了相关任务的概念,并按照功能的不同对相关任务的类型进行划分后再对它们的特点进行逐一描述。然后,本文按照数据处理模式和任务关系建模过程的不同将当前的主流算法划分为两大类:结构化多任务学习算法和深度多任务学习算法。

其中,结构化多任务学习算法采用线性模型,可以直接针对数据进行结构假设并且使用原有标注特征表述任务关系,同时,又可根据学习对象的不同将其细分为基于任务层面和基于特征层面两种不同结构,每种结构有判别式方法和生成式方法两种实现手段。与结构化多任务学习算法的建模过程不同,深度多任务学习算法利用经过多层特征抽象后的深层次信息进行任务关系描述,通过处理特定网络层中的参数达到信息共享的目的。紧接着,以两大类算法作为主线,本文详细分析了不同建模方法中对任务关系的结构假设、实现途径、各自的优缺点以及方法之间的联系。

最后,本文总结了任务之间相似性及其紧密程度的判别依据,并且分析了多任务作用机制的有效性和内在成因,从归纳偏置和动态求解等角度阐述了多任务信息迁移的特点。

基于研究生阶段的学习和研究，将自己所理解到的知识进行一个记录分享。文中提及的都是个人认为核心的主线，理解清楚能拓展到其他的多目标优化算法。文中或许有些许错误，思虑不周，还望海涵。

如果存在若干相互冲突的目标并需要同时处理，即成为多目标优化问题（Multi-objective Optimization Problems, MOPs）。对于MOPs，不可能使得所有的目标同时达到最优状态，只能得到一组均衡解，称之为Pareto最优集合。进化算法（Evolutionary algorithm，EA）是一类基于群体搜索的随机优化方法。EA运行一次可以获得一组解，而且对待复杂问题的数学性质不做严格假设，因而被广泛地应用于求解各类MOPs，并因此产生了许多经典的多目标进化算法（Multi-objective evolutionary algorithm，MOEA）。

非常重要的概念：对于所有子目标，若解xa不比解xb差，且xa至少有一个子目标比解xb好(好坏从目标空间取值来看，下文会举例说明)，则称xa支配xb，称xa为非支配解，xb为支配解。若没有解支配xa，则称xa为Pareto最优解。所有Pareto最优解组成的集合被称为Pareto最优集合(Pareto Set,PS)。Pareto最优集合在目标空间的映射称为Pareto前沿(Pareto Front,PF)。

还是举例能最直接清楚阐述问题。首先单独来看，目标 f1和 f2都是单目标最优化问题，最优解分别为x=0和x=1（多目标优化中一般以最小化为最优目标）。但是对于多目标优化来说，最优解并不是一个具体的数值对，而是一组Pareto(帕累托)最优解，即PS。

注：PS是决策空间，也就是变量x；PF是PS在目标空间的映射，也就是目标 f1和 f2。

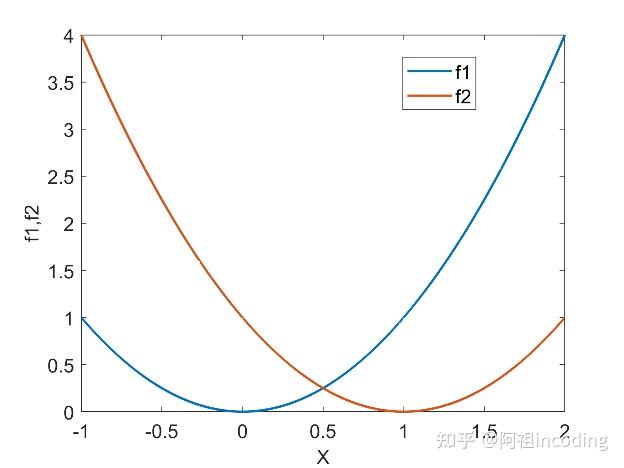
说明：由图1可以看出没有解可以使f1和 f2同时最小。当一个子目标达到最优时，另一个目标并不是最优。因此，当x?[0,1]时，两个函数达成折衷解，称x?[0,1]为PS。

那估计有家人们要问，其他x取值就不是PS了吗？

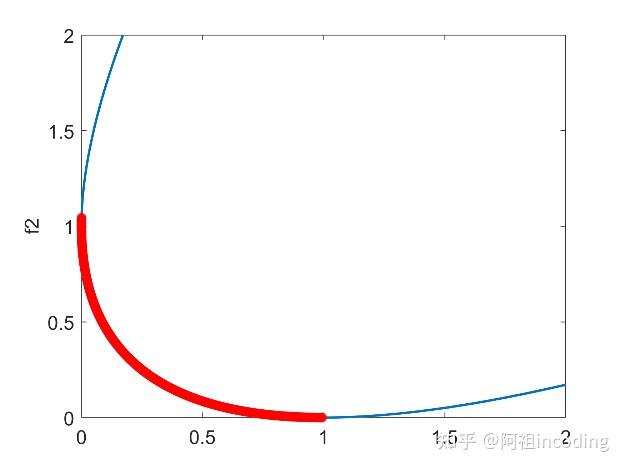
显然不是，找个反例就能解释这种情况。例如，x=2就不是Pareto最优解，因为此时的两个函数的取值都没有x=1时好。设x1，x2?[0,1]，x3?[0,1]；显然，x1,x2没有被其他解支配，它们互为非支配解。x1，x2支配x3，x3为支配解。图2中加粗部分为此问题的PF。

这一节主要说明了什么是多目标优化问题，以及多目标相关的基础概念。讲到这里核心的基本概念就说完了，清晰明了吧。提出问题之后就得解决问题，那如何解决问题，请看下回分解。

有问题请随时指正。

非支配教学优化算法（non-dominated sorting teaching–learning-based optimization algorithm，NSTLBO）由 R.Venkata Rao等人于2018年提出。

NSTLBO算法流程如下：

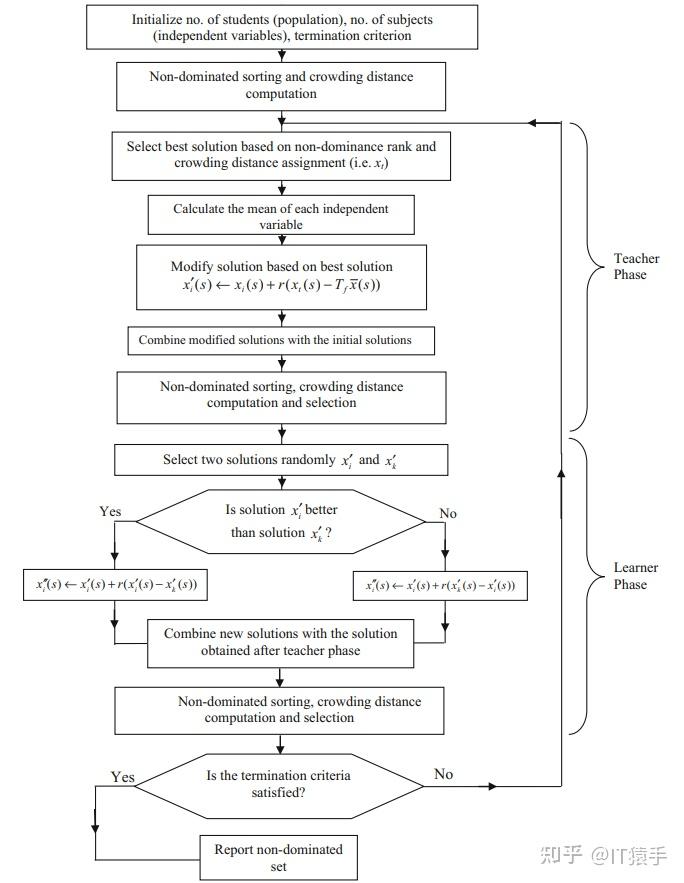
将NSTLBO在46个多目标测试函数（ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3）以及1个工程应用（盘式制动器设计）上实验,并采用IGD、GD、HV、SP进行评价

部分实验结果如下：

ZDT1：

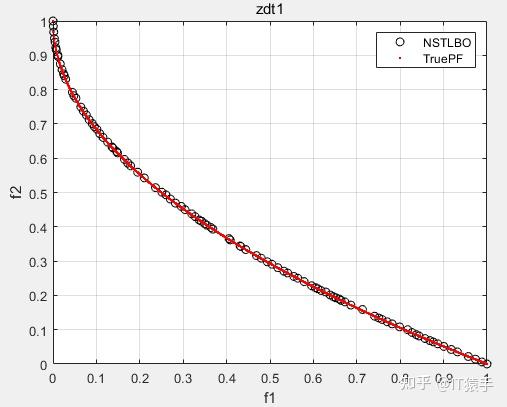
ZDT2：

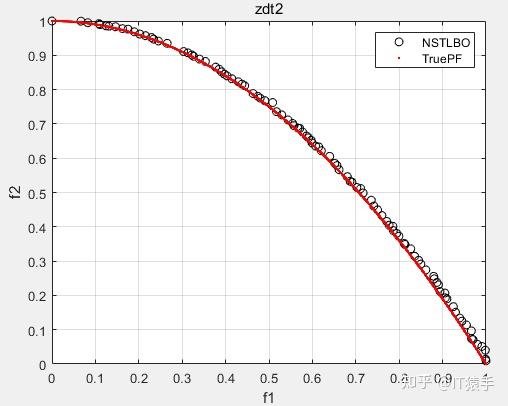
Viennet3：

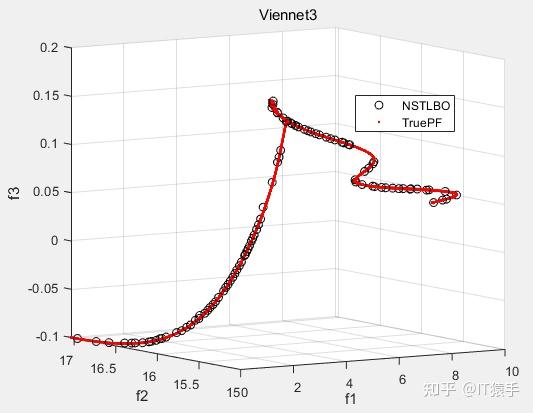
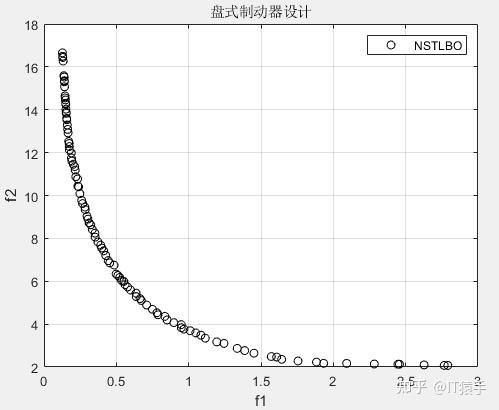
盘式制动器设计：