如何用python写优化器？

我想用 python 写一个 sgdm 的优化器，我需要学习什么知识，程序的构建需要注意哪些细节

要编写一个随机梯度下降（SGD）的优化器，首先你需要了解以下概念：

1. 梯度下降法（Gradient Descent）：这是一种迭代方法，用于找到函数的局部最小值。在每一步，我们都会沿着函数梯度（或者是上升最快的方向）的相反方向进行一步，以此来减小函数值。

2. 随机梯度下降（Stochastic Gradient Descent）：SGD 是基于梯度下降的一个改进版本，其中在每一步中只随机选择一个样本来计算梯度，而不是使用全部数据。这使得 SGD 在处理大规模数据集时更高效。

3. 深度学习与神经网络：理解深度学习和神经网络的基本原理是必要的，因为 SGD 经常用于训练这些模型。

4. 自动求导机制：理解如何使用 Python 的深度学习库（如 PyTorch 或 TensorFlow）中的自动求导机制，以方便计算梯度。

5. 学习率调整：理解如何设置和调整学习率。这是影响优化器性能的关键因素。

以下是一个简单的 SGD 优化器的例子，为了简化，我们假设输入参数 `params` 是一个一维的 NumPy 数组：

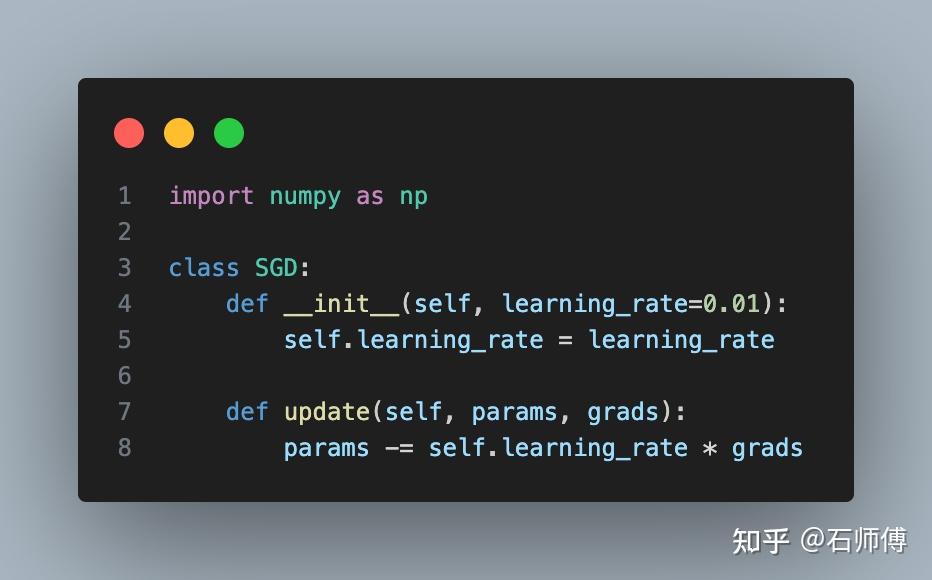
以下是如何使用此优化器的例子：

这只是最基本的 SGD 优化器，实际使用时可能需要添加一些额外的功能，例如动量（momentum）或学习率衰减等。

如果进一步优化动量和学习率：

1. 动量：动量在优化算法中可以帮助加速 SGD 在相关方向上的收敛，并抑制振荡，达到更快的收敛速度。它通过积累之前梯度的指数加权平均来实现，可以想象为下坡滚球的物理过程。

2. 学习率衰减：在训练的过程中，随着接近最小值点，我们可能希望慢慢减小学习率以更好地收敛。这就是学习率衰减的思想。

以下是一个带有动量和学习率衰减的 SGD 优化器的实现：

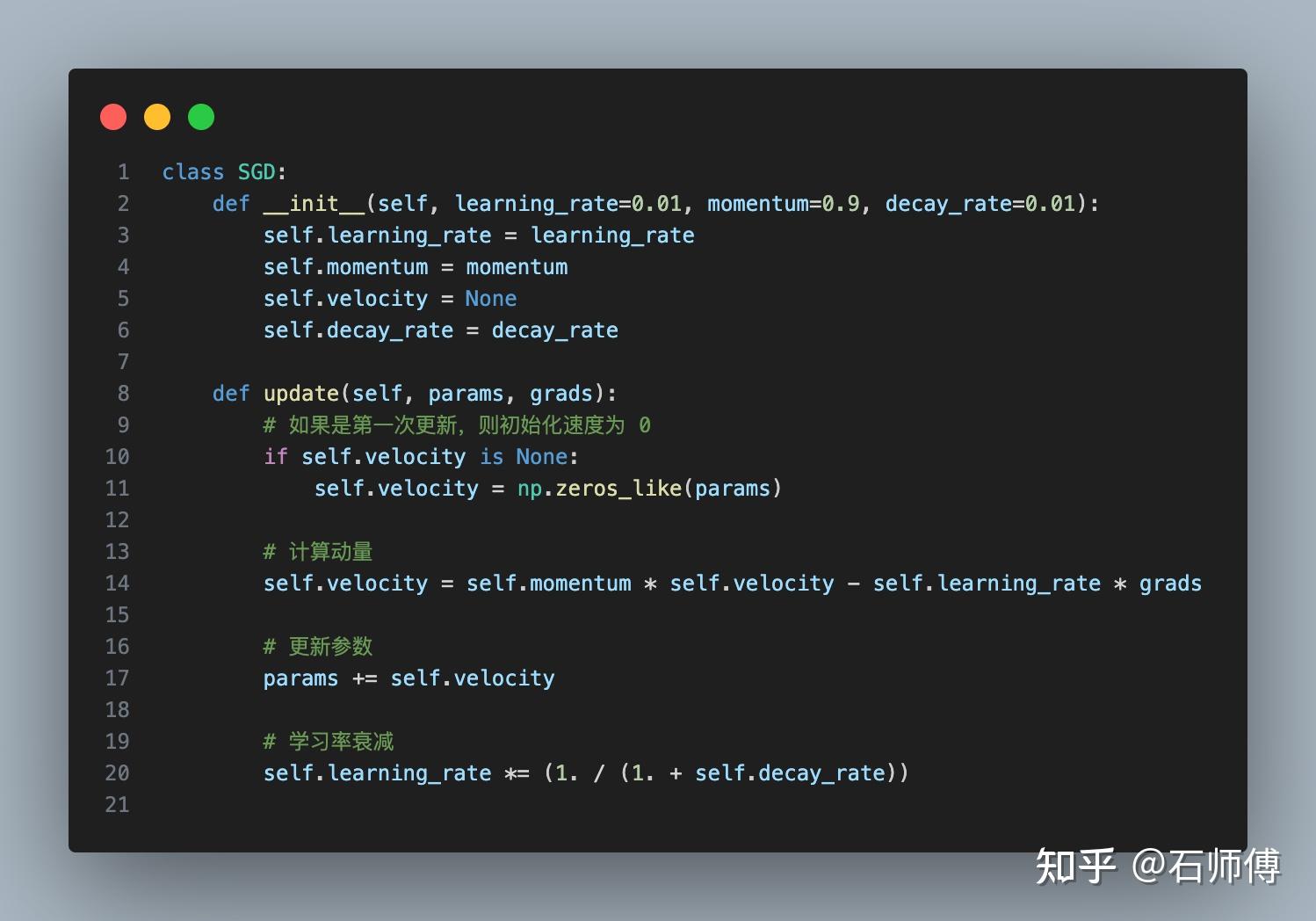
使用这个优化器的方法和之前的例子类似，只是现在加入了新的参数：

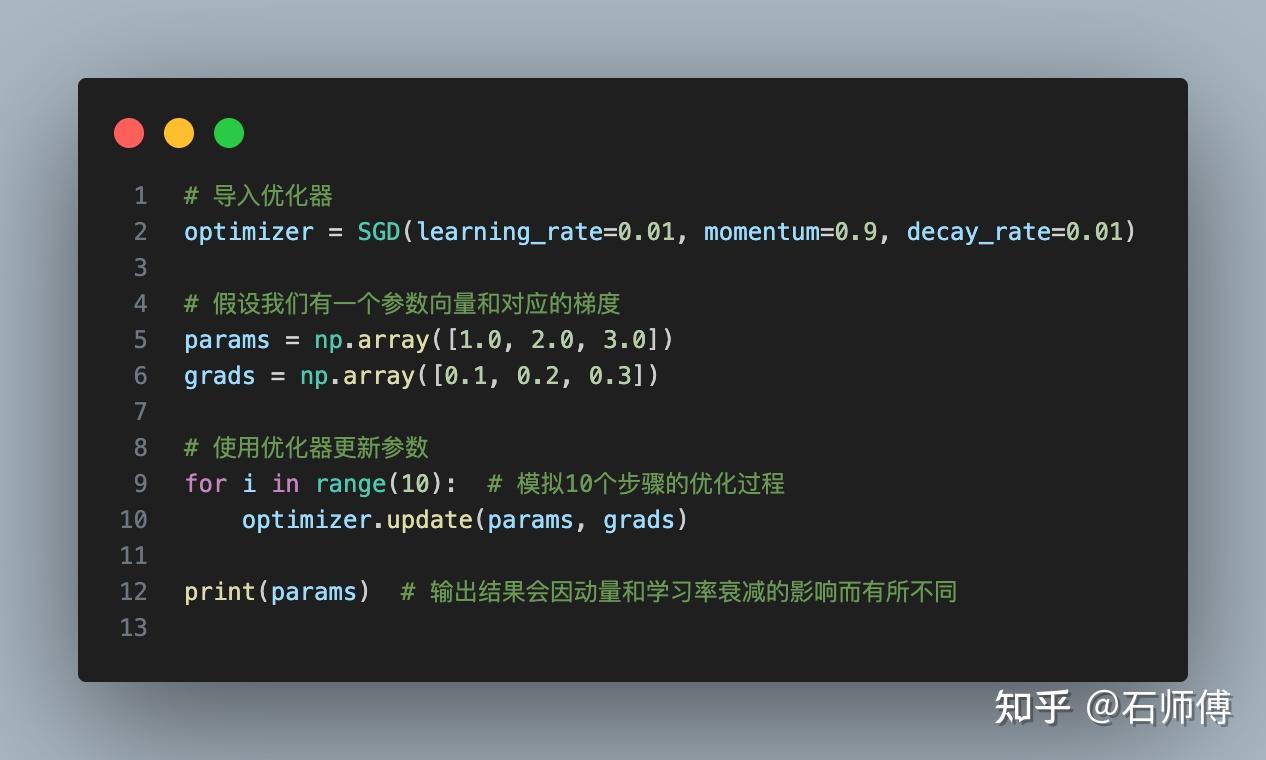
这个简单的代码只适用于一维的参数，如果要处理高维参数（例如在神经网络中），则需要稍作修改。

此外，编写优化器需要注意正确地实现梯度计算和参数更新，同时要确保代码的效率，因为优化器可能会在大量的参数和数据上运行。

import numpy as np

def gradient_descent_optimizer(func, dfunc, initial_x, learning_rate=0.1, epochs=1000, tolerance=1e-6):
    """
    梯度下降优化器的实现

    参数：
        func: 要优化的函数
        dfunc: func的导数
        initial_x: 初始优化变量的值
        learning_rate: 学习率（步长）
        epochs: 最大迭代次数
        tolerance: 收敛判断的容忍度

    返回：
        最优解x的值
    """
    x=initial_x

    for epoch in range(epochs):
        gradient=dfunc(x)
        new_x=x - learning_rate * gradient

        # 判断是否收敛
        if np.abs(new_x - x) < tolerance:
            break

        x=new_x

    return x

# 示例：优化函数 f(x)=x^2
def func(x):
    return x**2

# f(x)的导数 df(x)=2x
def dfunc(x):
    return 2*x

# 调用优化器进行优化
initial_x=5  # 初始变量值
learning_rate=0.1
epochs=1000
optimal_x=gradient_descent_optimizer(func, dfunc, initial_x, learning_rate, epochs)

print("最优解 x=", optimal_x)
print("最优解 f(x)=", func(optimal_x))

梯度下降优化器的实现。