前面几篇中,我们介绍了优化算法的框架,在框架的基础上实现了粒子群算法,并找了测试函数来进行测试。可以看出,基于框架来实现优化算法还是挺复杂的,那么为什么要做的这么复杂呢?当然是为了方便改进和实现新算法。
下面将实现粒子群算法的改进,作为例子,看看如何改进优化算法。
需要已实现的代码,可在
中找到。
| 文件名 | 描述 |
|---|---|
| ..\\optimization algorithm\\frame\\Unit.m | 个体 |
| ..\\optimization algorithm\\frame\\Algorithm_Impl.m | 算法主体 |
| ..\\optimization algorithm\\frame\\Get_Functions_details.m | 测试函数,求值用 |
| ..\\optimization algorithm\\frame\\func_plot.m | 函数图像,画图用 |
| ..\\optimization algorithm\\algorithm_particle_swarm\\PSO_Unit.m | 粒子群算法个体 |
| ..\\optimization algorithm\\algorithm_particle_swarm\\PSO_Base.m | 粒子群算法主体 |
| ..\\optimization algorithm\\algorithm_particle_swarm\\PSO_Impl.m | 粒子群算法实现 |
改进方式:惯性系数W,随着迭代次数,从1线性递减至0。
..\\optimization algorithm\\algorithm_particle_swarm\\PSO_Impl_1.m
% PSO修改,惯性系数W线性递减,由1->0
classdef PSO_Impl_1 < PSO_Base
% 外部可调用的方法
methods
function self = PSO_Impl_1(dim,size,iter_max,range_min_list,range_max_list)
% 调用父类构造函数设置参数
self@PSO_Base(dim,size,iter_max,range_min_list,range_max_list);
self.name = 'PSO_1';
end
end
% 重写父类的方法
methods (Access = protected)
% 每一代的更新
function update(self,iter)
update@PSO_Base(self,iter)
% 惯性系数线性递减,由1->0
self.W = (1.0-iter/self.iter_max);
end
end
end这样就实现好了,是不是非常的简单。因为面向对象编程,只需要实现修改的部分就好了,相同的部分不用动。这样也大大降低了出错的概率。
下面进行测试,只需要将Test.m中的PSO_Impl改成PSO_Impl_1即可
下面来修改测试代码
%% 清理之前的数据
% 清除所有数据
clear all;
% 清除窗口输出
clc;
%% 添加框架路径
% 将上级目录中的frame文件夹加入路径
addpath('https://zhuanlan.zhihu.com/frame')
%% 选择测试函数
Function_name='F1';
%[最小值,最大值,维度,测试函数]
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
%% 算法实例
% 种群数量
size = 50;
% 最大迭代次数
iter_max = 1000;
% 取值范围上界
range_max_list = ones(1,dim)*ub;
% 取值范围下界
range_min_list = ones(1,dim)*lb;
% 实例化粒子群类
base = PSO_Impl_1(dim,size,iter_max,range_min_list,range_max_list);
% 告诉算法求不是求最大值
base.is_cal_max = false;
% 确定适应度函数
base.fitfunction = fobj;
% 运行
base.run();
%% 绘制图像
figure('Position',[500 500 660 290])
% Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
% Draw objective space
subplot(1,2,2);
% 绘制曲线
semilogy(base.value_best_history,'Color','r')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
% 将坐标轴调整为紧凑型
axis tight
% 添加网格
grid on
% 四边都显示刻度
box off
legend(base.name)
display(['The best solution obtained by ',base.name ,' is ', num2str(base.value_best)]);
display(['The best optimal value of the objective funciton found by ',base.name ,' is ', num2str(base.position_best)]);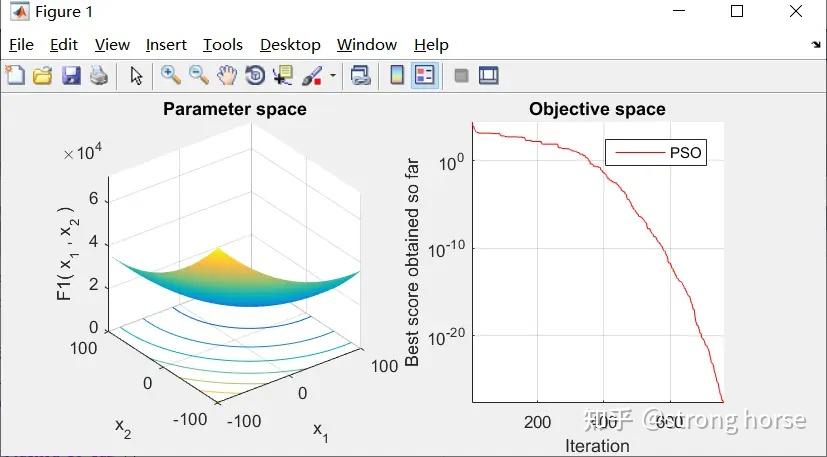
那么现在我们想比较一下PSO和PSO_1,相把曲线画在一张图中,该怎么做呢?上代码
%% 清理之前的数据
% 清除所有数据
clear all;
% 清除窗口输出
clc;
%% 添加框架路径
% 将上级目录中的frame文件夹加入路径
addpath('https://zhuanlan.zhihu.com/frame')
%% 选择测试函数
Function_name='F1';
%[最小值,最大值,维度,测试函数]
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
%% 算法实例
% 种群数量
size = 50;
% 最大迭代次数
iter_max = 1000;
% 取值范围上界
range_max_list = ones(1,dim)*ub;
% 取值范围下界
range_min_list = ones(1,dim)*lb;
% 实例化粒子群PSO_Impl
base = PSO_Impl(dim,size,iter_max,range_min_list,range_max_list);
%告诉算法求不是求最大值
base.is_cal_max = false;
% 确定适应度函数
base.fitfunction = fobj;
% 运行
base.run();
% 实例化粒子群类PSO_Impl_1
base_1 = PSO_Impl_1(dim,size,iter_max,range_min_list,range_max_list);
%告诉算法求不是求最大值
base_1.is_cal_max = false;
% 确定适应度函数
base_1.fitfunction = fobj;
% 运行
base_1.run();
%% 绘制图像
figure('Position',[500 500 660 290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
%Draw objective space
subplot(1,2,2);
% 绘制曲线,由于算法是求最大值,适应度函数为求最小值,故乘了-1,此时去掉-1
h1 = semilogy(base.value_best_history,'Color','r');
hold on
h2 = semilogy(base_1.value_best_history,'Color','b');
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
% 将坐标轴调整为紧凑型
axis tight
% 添加网格
grid on
% 四边都显示刻度
box off
legend([h1,h2],base.name,base_1.name)
display(['The best solution obtained by ',base.name ,' is ', num2str(base.value_best)]);
display(['The best optimal value of the objective funciton found by ',base.name ,' is ', num2str(base.position_best)]);
display(['The best solution obtained by ',base_1.name ,' is ', num2str(base_1.value_best)]);
display(['The best optimal value of the objective funciton found by ',base_1.name ,' is ', num2str(base_1.position_best)]);得到如下图像
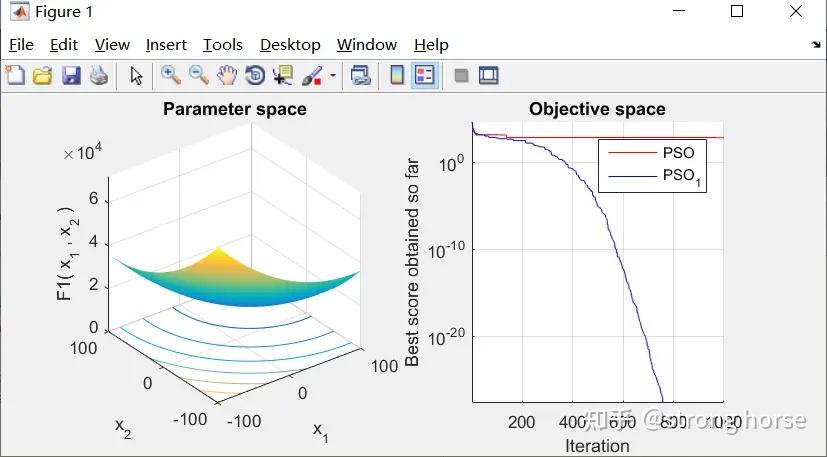
公司名称: 天富娱乐-天富医疗器械销售公司
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号